题目内容
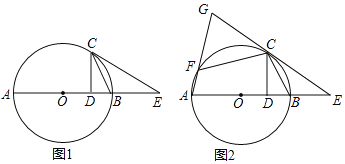
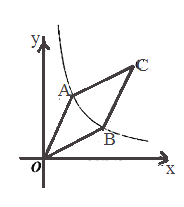
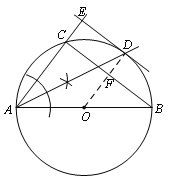
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,过点A作AD平分∠BAC,交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.

(1)依据题意,补全图形(尺规作图,保留痕迹);
(2)判断并证明:直线DE与⊙O的位置关系;
(3)若AB=10,BC=8,求CE的长.
【答案】(1)见解析;(2) 直线DE是⊙O的切线,证明见解析;(3)2.3或4.2
【解析】
(1)依据题意,利用尺规作图技巧补全图形即可;
(2)由题意连结OD,交BC于F,判断并证明OD⊥DE于D以此证明直线DE与⊙O的位置关系;
(3)由题意根据相关条件证明平行四边形CFDE是矩形,从而进行分析求解.
(1)如图.
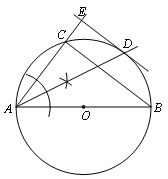
(2)判断:直线DE是⊙O的切线.
证明:连结OD,交BC于F.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∴![]() .
.
∴OD⊥BC于F.
∵DE∥BC,
∴OD⊥DE于D.
∴直线DE是⊙O的切线.
(3)∵AB是⊙O的直径,
∴∠ACB=90°.
∵AB=10,BC=8,
∴AC=6.
∵∠BOF=∠ACB=90°,
∴OD∥AC.
∵O是AB中点,
∴OF=![]() =3.
=3.
∵OD=![]() =5,
=5,
∴DF=2.
∵DE∥BC,OD∥AC,
∴四边形CFDE是平行四边形.
∵∠ODE=90°,
∴平行四边形CFDE是矩形.
∴CE=DF=2.

 尖子生新课堂课时作业系列答案
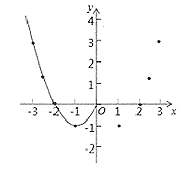
尖子生新课堂课时作业系列答案【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:其中,
的几组对应值列表如下:其中,![]() .
.
| …… |
|
|
|
| 0 | 1 | 2 |
| 3 | …… |
| …… | 3 |
|
|
| 0 |
| 0 |
| 3 | …… |
(2)根据表中数据,在如图所示的平面直角坐标系中描点,已画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出一条函数的性质: ;
(4)观察函数图象发现:若关于![]() 的方程
的方程![]() 有4个实数根,则
有4个实数根,则![]() 的取值范围是 .
的取值范围是 .