题目内容
7.(1)解方程组:$\left\{\begin{array}{l}{3x-y=-7}\\{y+4z=3}\\{2x-2z=-5}\end{array}\right.$(2)解不等式,并把解在数轴上表示出来
x-$\frac{1}{2}$[x-$\frac{1}{2}$(x-1)]<$\frac{2}{3}$(x-1).
分析 (1)加减消元法解之即可;
(2)先去括号,再去分母、移项、合并同类项即可得.
解答 解:(1)解方程组$\left\{\begin{array}{l}{3x-y=-7}&{①}\\{y+4z=3}&{②}\\{2x-2z=-5}&{③}\end{array}\right.$,
①+②,得:3x+4z=-4 ④,
③×2+④,得:7x=-14,解得x=-2,
将x=2代入①,得:-6-y=-7,解得y=1,
将y=1代入②,得:1+4z=3,解得:z=$\frac{1}{2}$,
∴方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=1}\\{z=\frac{1}{2}}\end{array}\right.$;
(2)去括号,得:x-$\frac{1}{2}$x+$\frac{1}{4}$(x-1)<$\frac{2}{3}$x-$\frac{2}{3}$,
x-$\frac{1}{2}$x+$\frac{1}{4}$x-$\frac{1}{4}$<$\frac{2}{3}$x-$\frac{2}{3}$,
去分母,得:12x-6x+3x-3<8x-8,
移项、合并,得:x<-5,
表示在数轴上如下:
点评 本题主要考查解方程组和解不等式的能力,熟练掌握加减消元法是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
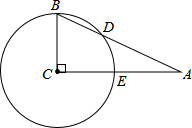 如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E. 如图,已知CD是△ABC的中线,AC=9cm,BC=3cm,那么△ACD和△BCD的周长之差是多少?
如图,已知CD是△ABC的中线,AC=9cm,BC=3cm,那么△ACD和△BCD的周长之差是多少? 如图,在平面直角坐标系中,点A是y轴上的一点,点B与点C在x轴上且关于原点对称,若点A(0,3),点B(-4,0).
如图,在平面直角坐标系中,点A是y轴上的一点,点B与点C在x轴上且关于原点对称,若点A(0,3),点B(-4,0).