题目内容
把下列函数化为y=a(x+m)2+k形式,并求出各函数图象的顶点坐标、对称轴、最大值或最小值:
(1)y=x2-2x+4;
(2)y=100-5x2.
(1)y=x2-2x+4;
(2)y=100-5x2.
考点:二次函数的三种形式
专题:
分析:利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,可把一般式转化为顶点式,从而求出函数图象的对称轴及顶点坐标及最值.
解答:解:(1)y=x2-2x+4=x2-2x+1+3=(x-1)2+3.
顶点坐标是(1,-1),对称轴为x=1,最小值为-1;
(2)y=100-5x2.
顶点坐标是(0,100),对称轴为x=0,最大值为100.
顶点坐标是(1,-1),对称轴为x=1,最小值为-1;
(2)y=100-5x2.
顶点坐标是(0,100),对称轴为x=0,最大值为100.
点评:本题主要考查了利用配方法将一般式转化为顶点式的方法以及函数图象的对称轴、顶点坐标公式.

练习册系列答案
相关题目
 如图,二次函数y=x2+bx+c的图象与x轴的负半轴相交于A、B两点,与y轴的正半轴相交于点C,与函数y=
如图,二次函数y=x2+bx+c的图象与x轴的负半轴相交于A、B两点,与y轴的正半轴相交于点C,与函数y=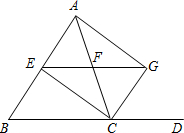 如图,E、F分别是AB、AC的中点,延长EF交∠ACD的平分线于点G.AG与CG有怎样的位置关系?说明你的理由.
如图,E、F分别是AB、AC的中点,延长EF交∠ACD的平分线于点G.AG与CG有怎样的位置关系?说明你的理由. 你听说过意大利著名的“比萨斜塔”吗?某人曾经从55m高的塔顶放下一个物体,它的着地点距塔底4.8m,斜塔偏离竖直线的角度是多少(精确到1′)?
你听说过意大利著名的“比萨斜塔”吗?某人曾经从55m高的塔顶放下一个物体,它的着地点距塔底4.8m,斜塔偏离竖直线的角度是多少(精确到1′)? 如图:AB∥CD,∠ABF=∠DCE.求证:∠BFE=∠FEC.
如图:AB∥CD,∠ABF=∠DCE.求证:∠BFE=∠FEC.