题目内容
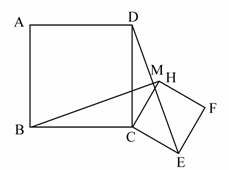
准备一张矩形纸片,按如图操作:
将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.

(1)证明:∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∴∠EBD=∠FDB,
∴EB∥DF,
∵ED∥BF,
∴四边形BFDE为平行四边形.
(2)解:∵四边形BFDE为菱形,
∴BE=ED,∠EBD=∠FBD=∠ABE,
∵四边形ABCD是矩形,
∴AD=BC,∠ABC=90°,
∴∠ABE=30°,
∵∠A=90°,AB=2,
∴AE= =
= ,BF=BE=2AE=
,BF=BE=2AE= ,
,
∴菱形BFDE的面积为: ×2=
×2=

练习册系列答案
相关题目
某商场购进一批服装,每件进价为200元,由于换季滞销,商场决定将这种服装按标价的六折销售,若打折后每件服装仍能获利20%,则该服装标价是( )
|
| A. | 350元 | B. | 400元 | C. | 450元 | D. | 500元 |
抛物线y=2x2,y=﹣2x2, 共有的性质是( )
共有的性质是( )
|
| A. | 开口向下 | B. | 对称轴是y轴 |
|
| C. | 都有最低点 | D. | y随x的增大而减小 |
下列计算正确的是( )
|
| A. | ﹣(﹣3)2=9 | B. |
| C. | ﹣(﹣2)0=1 | D. | |﹣3|=﹣3 |

 的图象经过点(﹣1,2),则k的值是
的图象经过点(﹣1,2),则k的值是  ﹣
﹣ )•(x﹣1),其中x=2.
)•(x﹣1),其中x=2. =3
=3