��Ŀ����
����Ŀ����Rt��ABC�У���ACB=90�㣬BC=30��AB=50����P��AB��������һ�㣬ֱ��PE��AB�����AC��BC�ཻ��E����M���߶�AP�ϣ���N���߶�BP�ϣ�EM=EN��sin��EMP= ![]() ��
��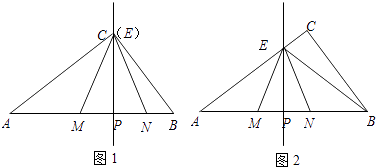
��1����ͼ1������E���C�غ�ʱ����CM�ij���
��2����ͼ2������E�ڱ�AC��ʱ����E�����A��C�غϣ���AP=x��BN=y����y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��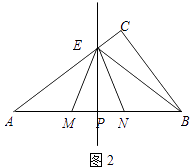
��3������AME�ס�ENB����AP�ij���
���𰸡�
��1��
�⣺�ߡ�ACB=90�㣬
��AC= ![]() =
= ![]() =40��
=40��
��CP��AB��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��CP=24��
��CM= ![]() =
= ![]() =26
=26
��2��
�⣺��sin��EMP= ![]() ��
��
����EP=12a��
��EM=13a��PM=5a��
��EM=EN��
��EN=13a��PN=5a��
�ߡ�AEP�ס�ABC��
�� ![]() ��
��
�� ![]() =
= ![]()
��x=16a��
��a= ![]() ��
��
��BP=50��16a��
��y=50��21a��
=50��21�� ![]() ��
��
=50�� ![]() x��
x��
�ߵ�E����A���غ�ʱ��x=0����E����C���غ�ʱ��x=32��
�ຯ���Ķ������ǣ���0��x��32��
��3��
�⣺�ٵ���E��AC��ʱ����ͼ2��
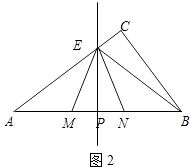
��EP=12a����EM=13a��MP=NP=5a��
�ߡ�AEP�ס�ABC��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��AP=16a��
��AM=11a��
��BN=50��16a��5a=50��21a��
�ߡ�AME�ס�ENB��
�� ![]() =
= ![]()
�� ![]() =
= ![]() ��
��
��a= ![]() ��
��
��AP=16�� ![]() =22��
=22��
�ڵ���E��BC��ʱ����ͼ������ͼ������EP=12a����EM=13a��MP=NP=5a��
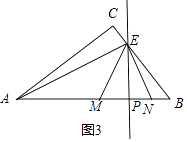
�ߡ�EBP�ס�ABC��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
���BP=9a��
��BN=9a��5a=4a��AM=50��9a��5a=50��14a��
�ߡ�AME�ס�ENB��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
���a= ![]() ��
��
��AP=50��9a=50��9�� ![]() =42��
=42��
����AP�ij���22��42��
������������1���������ȸ�����֪�����ó�AC��ֵ���ٸ���CP��AB���CP���Ӷ��ó�CM��ֵ����2���������ȸ���EN������sin��EMP= ![]() �����EP��ֵ���Ӷ��ó�EM��PM��ֵ���ٵó���AEP�ס�ABC���������
�����EP��ֵ���Ӷ��ó�EM��PM��ֵ���ٵó���AEP�ס�ABC��������� ![]() =
= ![]() �����a��ֵ�����ɵó�y����x�ĺ�����ϵʽ����������������Ķ�����3������������EP��ֵ���ó���EM��MP��ֵ��Ȼ��֢ٵ�E��AC��ʱ�����ݡ�AEP�ס�ABC�����AP��ֵ���Ӷ��ó�AM��BN��ֵ���ٸ��ݡ�AME�ס�ENB�����a��ֵ���ó�AP�ij����ڵ�E��BC��ʱ�����ݡ�EBP�ס�ABCC�����AP��ֵ���Ӷ��ó�AM��BN��ֵ���ٸ��ݡ�AME�ס�ENB�����a��ֵ���ó�AP�ij���
�����a��ֵ�����ɵó�y����x�ĺ�����ϵʽ����������������Ķ�����3������������EP��ֵ���ó���EM��MP��ֵ��Ȼ��֢ٵ�E��AC��ʱ�����ݡ�AEP�ס�ABC�����AP��ֵ���Ӷ��ó�AM��BN��ֵ���ٸ��ݡ�AME�ס�ENB�����a��ֵ���ó�AP�ij����ڵ�E��BC��ʱ�����ݡ�EBP�ס�ABCC�����AP��ֵ���Ӷ��ó�AM��BN��ֵ���ٸ��ݡ�AME�ס�ENB�����a��ֵ���ó�AP�ij���
�����㾫����������Ҫ���������������ε�Ӧ�õ����֪ʶ�㣬��Ҫ���ղ�ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������������ȷ�����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�