题目内容
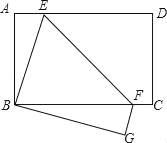
【题目】如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( ) 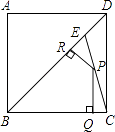
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:连接BP,过C作CM⊥BD,如图所示: 
∵BC=BE,
∴S△BCE=S△BPE+S△BPC
= ![]() BC×PQ+
BC×PQ+ ![]() BE×PR=
BE×PR= ![]() BC×(PQ+PR)=
BC×(PQ+PR)= ![]() BE×CM,
BE×CM,
∴PQ+PR=CM,
∵四边形ABCD是正方形,
∴∠BCD=90°,CD=BC=1,∠CBD=∠CDB=45°,
∴BD= ![]() =
= ![]() ,
,
∵BC=CD,CM⊥BD,
∴M为BD中点,
∴CM= ![]() BD=
BD= ![]() ,
,
即PQ+PR值是 ![]() .
.
故选:C.
【考点精析】本题主要考查了等腰三角形的性质和正方形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目