题目内容
二次函数y=ax2+bx+c(a为常数,且a≠0)的图象过点A(0,1),B(1,﹣2)和C(3,﹣2).
(1)求二次函数表达式;
(2)若m>n>2,比较m2﹣4m与n2﹣4n的大小;
(3)将抛物线y=ax2+bx+c平移,平移后图象的顶点为(h,k),若平移后的抛物线与直线y=x﹣1有且只有一个公共点,请用含h的代数式表示k.
【考点】待定系数法求二次函数解析式;二次函数图象与几何变换.
【专题】计算题.
【分析】(1)把A、B、C点坐标分别代入y=ax2+bx+c得到关于a、b、c的方程组,然后解方程组求出a、b、c即可得到抛物线解析式;
(2)先确定抛物线对称轴方程,然后二次函数的性质,当m>n>2,m2﹣4m+1>n2﹣4n+1,整理得到m2﹣4m>n2﹣4n;
(3)设平移后的抛物线的表达式为y=(x﹣h)2+k,由于直线y=x﹣1与抛物线有且只有一个公共点,则说明方程x﹣1=(x﹣h)2+k有两个相等的实数根,然后把方程整理为一般式后△=0即可得到h与k的关系式.
【解答】解:(1)∵抛物线过点A(0,1),B(1,﹣2)和C(3,﹣2).
∴ ,解得
,解得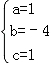
∴抛物线解析式为y=x2﹣4x+1;
(2)∵y=(x﹣2)2﹣3,
∴抛物线的对称轴为直线x=2,
∵m>n>2,
∴m2﹣4m+1>n2﹣4n+1,
∴m2﹣4m>n2﹣4n;
(3)设平移后的抛物线的表达式为y=(x﹣h)2+k,
∵直线y=x﹣1与抛物线有且只有一个公共点,
∴方程x﹣1=(x﹣h)2+k有两个相等的实数根.
整理得x2﹣(2h+1)x+h2+k+1=0,
∴△=(2h+1)2﹣4(h2+k+1)=0,
∴k=h﹣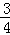 .
.
【点评】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了抛物线与直线的交点问题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案
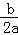 与反比例函数y=
与反比例函数y=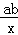 在同一坐标系内的大致图象是( )
在同一坐标系内的大致图象是( )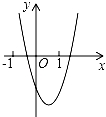
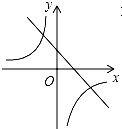 B.
B.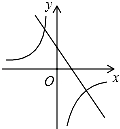 C.
C.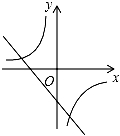 D.
D.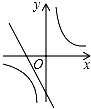
 C的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
C的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.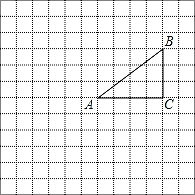


 B.
B. C.
C. D.
D.
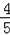
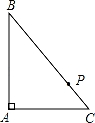
 ,则线段CE的最大值为 .
,则线段CE的最大值为 .