题目内容
 如图,已知菱形ABCD的两条对角线AC与BD交于平面直角坐标系的原点,且AD∥x轴,点A的坐标为(-2,3),则点B的坐标为
如图,已知菱形ABCD的两条对角线AC与BD交于平面直角坐标系的原点,且AD∥x轴,点A的坐标为(-2,3),则点B的坐标为
- A.(-3,-3)
- B.(-3,-4)
- C.(-4,-3)
- D.(-4.5,-3)
D
分析:设AD与y轴交点为E,根据点A的坐标求出AE、OE的长度,再根据菱形的对角线互相垂直可以判定△AOE与△DOE相似,然后根据相似三角形对应边成比例列式求出DE的长度,从而得到点D的坐标,最后根据点B与点D成中心对称解答.
解答: 解:如图,设AD与y轴交点为E,
解:如图,设AD与y轴交点为E,
∵点A的坐标为(-2,3),AD∥x轴,
∴AE=2,OE=3,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠AOE+∠DOE=90°,∠EAO+∠AOE=90°,
∴∠DOE=∠EAO,
又∵∠AEO=∠OED=90°,
∴△AOE∽△DOE,
∴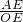 =
= ,
,
即 =
= ,
,
解得DE=4.5,
∴点D的坐标为(4.5,3),
∵点B与点D关于原点成中心对称,
∴点B的坐标为(-4.5,-3).
故选D.
点评:本题考查了菱形的性质和中心对称的性质以及相似三角形对应边成比例的性质,解题的关键是求出点D到y轴的距离.
分析:设AD与y轴交点为E,根据点A的坐标求出AE、OE的长度,再根据菱形的对角线互相垂直可以判定△AOE与△DOE相似,然后根据相似三角形对应边成比例列式求出DE的长度,从而得到点D的坐标,最后根据点B与点D成中心对称解答.
解答:
 解:如图,设AD与y轴交点为E,
解:如图,设AD与y轴交点为E,∵点A的坐标为(-2,3),AD∥x轴,
∴AE=2,OE=3,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠AOE+∠DOE=90°,∠EAO+∠AOE=90°,
∴∠DOE=∠EAO,
又∵∠AEO=∠OED=90°,
∴△AOE∽△DOE,
∴
 =
= ,
,即
 =
= ,
,解得DE=4.5,
∴点D的坐标为(4.5,3),
∵点B与点D关于原点成中心对称,
∴点B的坐标为(-4.5,-3).
故选D.
点评:本题考查了菱形的性质和中心对称的性质以及相似三角形对应边成比例的性质,解题的关键是求出点D到y轴的距离.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
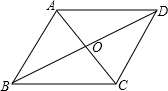 如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
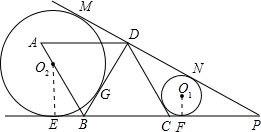 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G. 如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的
如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的