题目内容
11.计算:$\frac{{{x^2}+6x+9}}{{{x^2}-9}}$=$\frac{x+3}{x-3}$.分析 先将分子与分母进行因式分解,再约去它们的公因式,即可求解.
解答 解:$\frac{{{x^2}+6x+9}}{{{x^2}-9}}$=$\frac{(x+3)^{2}}{(x+3)(x-3)}$=$\frac{x+3}{x-3}$.
故答案为$\frac{x+3}{x-3}$.
点评 本题考查了约分的定义与方法.约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.由约分的概念可知,要首先将分子、分母转化为乘积的形式,再找出分子、分母的最大公因式并约去,注意不要忽视数字系数的约分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列命题中是真命题的是( )
| A. | 全等三角形的对应边相等 | |
| B. | 两直线平行,同旁内角相等 | |
| C. | 两个角相等,这两个角一定是对顶角 | |
| D. | 相等的两个角是平行线所得的内错角 |
16.下列方程中,是一元一次方程的是( )
| A. | x2-4x=3 | B. | 2x=0 | C. | x+2y=1 | D. | $x-1=\frac{1}{x}$ |
3.以下长度的三条线段,不能组成三角形的是( )
| A. | 9、15、7 | B. | 4、9、6 | C. | 15、20、6 | D. | 3、8、4 |
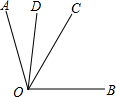 如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOD=25°,∠BOC=50°,∠AOB=100°.
如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOD=25°,∠BOC=50°,∠AOB=100°.