题目内容
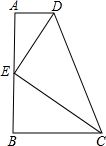 直角梯形ABCD中,∠A=∠B=90°,E在AB上,DE⊥EC,AD+DE=AB=8,那么△BCE的周长为________.
直角梯形ABCD中,∠A=∠B=90°,E在AB上,DE⊥EC,AD+DE=AB=8,那么△BCE的周长为________.
16
分析:设AD=x,则DE=8-x,利用勾股定理可求AE= =
= ,利用已知条件证明△ADE∽△BEC,再利用相似三角形的性质似三角形的周长之比等于相似比,即可求出△BCE的周长.
,利用已知条件证明△ADE∽△BEC,再利用相似三角形的性质似三角形的周长之比等于相似比,即可求出△BCE的周长.
解答:设AD=x,则DE=8-x,
在Rt△ADE中,AE= =
= ,
,
∵AB=8,
∴BE=AB-AE=8-
∵∠A=∠B=90°,DE⊥EC,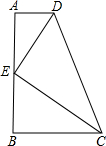
∴∠AED+∠ADE=90°,∠AED+∠BEC=90°,
∴∠ADE=∠BEC,
∴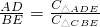 ,
,
∴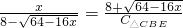 ,
,
∴△BCE的周长为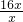 =16.
=16.
故答案为16.
点评:本题考查了直角梯形的性质、勾股定理的运用以及相似三角形的判定和性质,解题的关键是掌握相似三角形的周长之比等于相似比.
分析:设AD=x,则DE=8-x,利用勾股定理可求AE=
 =
= ,利用已知条件证明△ADE∽△BEC,再利用相似三角形的性质似三角形的周长之比等于相似比,即可求出△BCE的周长.
,利用已知条件证明△ADE∽△BEC,再利用相似三角形的性质似三角形的周长之比等于相似比,即可求出△BCE的周长.解答:设AD=x,则DE=8-x,
在Rt△ADE中,AE=
 =
= ,
,∵AB=8,
∴BE=AB-AE=8-

∵∠A=∠B=90°,DE⊥EC,

∴∠AED+∠ADE=90°,∠AED+∠BEC=90°,
∴∠ADE=∠BEC,
∴
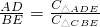 ,
,∴
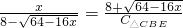 ,
,∴△BCE的周长为
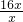 =16.
=16.故答案为16.
点评:本题考查了直角梯形的性质、勾股定理的运用以及相似三角形的判定和性质,解题的关键是掌握相似三角形的周长之比等于相似比.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
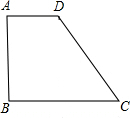 在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为
在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为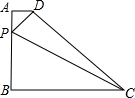 如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为
如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为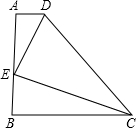 下结论:
下结论: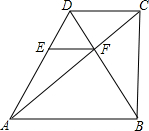 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.