题目内容
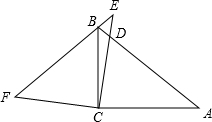 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△EFC的位置,其中E、F分别是A、B的对应点,且点B在斜边EF上,直角边EC交AB于点D,则∠ECA=
如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△EFC的位置,其中E、F分别是A、B的对应点,且点B在斜边EF上,直角边EC交AB于点D,则∠ECA=考点:旋转的性质
专题:
分析:根据直角三角形两锐角互余求出∠ABC=50°,再根据旋转的旋转可得∠F=∠ABC,CF=CB,∠BCF=∠ECA,再根据等腰三角形两底角相等求出∠BCF,即可得解.
解答:解:∵∠ACB=90°,∠A=40°,
∴∠ABC=90°-40°=50°,
∵△ABC旋转到△EFC的位置,点B在斜边EF上,
∴∠F=∠ABC=50°,CF=CB,∠BCF=∠ECA,
在△BCF中,∠BCF=180°-50°×2=80°,
∴∠ECA=80°.
故答案为:80.
∴∠ABC=90°-40°=50°,
∵△ABC旋转到△EFC的位置,点B在斜边EF上,
∴∠F=∠ABC=50°,CF=CB,∠BCF=∠ECA,
在△BCF中,∠BCF=180°-50°×2=80°,
∴∠ECA=80°.
故答案为:80.
点评:本题考查了旋转的性质,直角三角形两锐角互余,等腰三角形两底角相等的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中,真命题是( )
| A、两条对角线垂直且相等的四边形是正方形 |
| B、两条对角线互相垂直的四边形是菱形 |
| C、两条对角线互相平分且相等的四边形是矩形 |
| D、同一底上两个角相等的四边形是等腰梯形 |
已知单项式
的次数是8,则m的值是( )
| x2my3z |
| 7 |
| A、4 | B、3 | C、2 | D、1 |
已知4个式子:①|-
-
|;②|-
|-|-
|;③-
-|-
|;④-
-(-
),它们的值从小到大的顺是( )
| 3 |
| 5 |
| 4 |
| 7 |
| 3 |
| 5 |
| 4 |
| 7 |
| 3 |
| 5 |
| 4 |
| 7 |
| 3 |
| 5 |
| 4 |
| 7 |
| A、③<④<②<① |
| B、②<④<③<① |
| C、④<③<②<① |
| D、③<②<④<① |
 已知:如图,?ABCD中,E、F分别是CD、AB上的两点,且CE=AF.求证:BD、EF互相平分.
已知:如图,?ABCD中,E、F分别是CD、AB上的两点,且CE=AF.求证:BD、EF互相平分. 如图,在?ABCD中,对角线AC,BD交于点O,点E,点F在BD上,且 BE=DF 连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
如图,在?ABCD中,对角线AC,BD交于点O,点E,点F在BD上,且 BE=DF 连接AE并延长,交BC于点G,连接CF并延长,交AD于点H. 在图示的点阵中:
在图示的点阵中: