题目内容
11．如果抛物线y=ax2+bx+c（a≠0）经过点（-1，2）和（4，2），那么它的对称轴是直线x=$\frac{3}{2}$．分析 根据抛物线上函数值相等的点离对称轴的距离相等可求得答案．
解答 解：
∵抛物线y=ax2+bx+c（a≠0）经过点（-1，2）和（4，2），
∴对称轴为x=$\frac{-1+4}{2}$=$\frac{3}{2}$，
故答案为：x=$\frac{3}{2}$．
点评 本题主要考查二次函数的性质，掌握抛物线上函数值相等的点离对称轴的距离相等是解题的关键．
练习册系列答案
相关题目
△ABD与△EBC都是等腰直角三角形，AD、CE为斜边，延长EA、DC交于点F．
19．下列说法错误的是（ ）
| A． | 过圆上一点可以作一条直线和圆相切 | |
| B． | 过圆外一点可以作两条直线和圆相切 | |
| C． | 从圆外一点引圆的两条切线，它们的长相等 | |
| D． | 从圆外一点可以引圆的两条切线，切线长相等 |
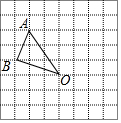如图，在边长为1的小正方形组成的网格中，△AOB的三个顶点均在格点上，O为原点，点A、B的坐标分别为A（-2，3）、B（-3，1）．
如图，在△ADE中，已知∠DAE=100°，DC=DA，EB=EA，则∠BAC的度数为40°．