题目内容
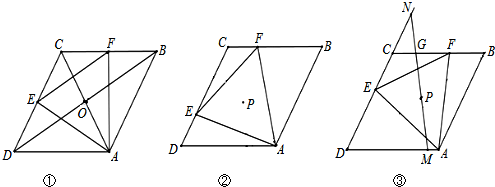
8. 为了测量停留在空中的气球的高度,小明先站在地面上某点处观测气球,测得仰角为30°,然后他向气球方向前进了40m,此时观测气球,测得仰角为60°,如图,点A、B表示小明两次观测气球时眼睛的位置,若小明的眼睛离地面1.5m,请你帮助他计算出气球的高度.(结果保留根号)
为了测量停留在空中的气球的高度,小明先站在地面上某点处观测气球,测得仰角为30°,然后他向气球方向前进了40m,此时观测气球,测得仰角为60°,如图,点A、B表示小明两次观测气球时眼睛的位置,若小明的眼睛离地面1.5m,请你帮助他计算出气球的高度.(结果保留根号)
分析 首先表示出CD,AD,BD的长,进而得出h的值,进而求出答案.
解答  解:如图,由题意知,∠CAD=30°,∠CBD=60°,AB=40m,
解:如图,由题意知,∠CAD=30°,∠CBD=60°,AB=40m,
点A、B、D在一条直线上,CD⊥AD,
设CD=hm.
在Rt△ACD中,AD=$\sqrt{3}$h,
在Rt△BCD中,BD=$\frac{\sqrt{3}}{3}$h,
所以,AB=$\sqrt{3}$h-$\frac{\sqrt{3}}{3}$h=$\frac{2\sqrt{3}}{3}$h=40,
解得:h=20$\sqrt{3}$,
所以气球的高度为:1.5+20$\sqrt{3}$m.
点评 此题主要考查了解直角三角形的应用,正确用未知数表示出各边长是解题关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
18.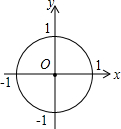 如图,在直角坐标系中,⊙O的半径是1,则直线y=-x+$\sqrt{2}$与⊙O的位置关系是( )
如图,在直角坐标系中,⊙O的半径是1,则直线y=-x+$\sqrt{2}$与⊙O的位置关系是( )
 如图,在直角坐标系中,⊙O的半径是1,则直线y=-x+$\sqrt{2}$与⊙O的位置关系是( )
如图,在直角坐标系中,⊙O的半径是1,则直线y=-x+$\sqrt{2}$与⊙O的位置关系是( )| A. | 相离 | B. | 相交 | ||
| C. | 相切,切点在第二象限 | D. | 相切,切点在第一象限 |
16.如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2012次输出的结果为( )


| A. | 3 | B. | 6 | C. | 32012 | D. | 62012 |
3.正n边形的内角和不大于1000°,则n不可能是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
20.估计我国人口的百万分之一是( )
| A. | 辽宁省人数 | B. | 丹东市人数 | C. | 某中学学生数 | D. | 我班人数 |