Question

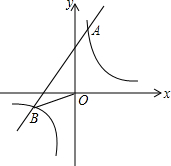如图，已知反比例函数y₁=

k

x

与一次函数y₂=ax+b的图象相交于两点A（1，3）B（n，-1）
（1）分别求出反比例函数与一次函数的函数关系式；
（2）观察图象，直接写出使得y₁＞y₂成立的自变量x的取值范围．

Answer 1

考点：反比例函数与一次函数的交点问题

专题：

分析：（1）把A代入反比例函数的解析式即可求得k的值，然后求得B的值，利用待定系数法即可求得一次函数的解析式；
（2）使得y₁＞y₂成立的自变量，即反比例函数的图象在一次函数的图象的上边，求得对应的自变量的范围即可．

解答：解：（1）把A（1，3）代入y=

k

x

得：k=3，则反比例函数的解析式是：y=

3

x

；
把B（n，-1）代入y=

3

x

得：-1=

3

n

，解得：n=-3，则B的坐标是（-3，-1）．
根据题意得：

a+b=3 -3a+b=-1

，
解得：

a=1 b=2

，
则一次函数的解析式是y=x+2；
（2）当x＜-3或0＜x＜1时，y₁＞y₂成立．

点评：本题主要考查了待定系数法求反比例函数与一次函数的解析式．这里体现了数形结合的思想．