题目内容
已知一直角梯形上下底分别为6，8，一腰长为7，则另一腰长a的值是________．
或3
分析：过点D作DE⊥BC于点E．则四边形ABED是矩形．在直角△DEC中根据勾股定理即可求得．
解答：
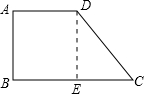解：过点D作DE⊥BC于点E，则四边形ABED是矩形，CE=BC-AD=8-6=2；当AB=7时，则DE=AB=7，在直角△DEC中，CD=
=
=；当CD=7时，在直角△DEC中，AB=DE=
=
=
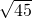=3；则另一腰长a的值是
或3．点评：通过作高线把直角梯形的问题转化为矩形和直角三角形的问题，是解决本题的关键．
练习册系列答案
相关题目
