题目内容
 如图,DE是过三角形ABC的顶点A的直线.
如图,DE是过三角形ABC的顶点A的直线.(1)当∠B=
∠DAB
∠DAB
时,DE∥BC,理由是内错角相等,两直线平行
内错角相等,两直线平行
.(2)当∠B+
∠EAB
∠EAB
=180°时,DE∥BC,理由是同旁内角互补,两直线平行
同旁内角互补,两直线平行
.分析:(1)根据内错角相等,两直线平行可得当∠B=∠DAB时,DE∥BC;
(2)根据同旁内角互补,两直线平行可得当∠B+∠EAB=180°时,DE∥BC.
(2)根据同旁内角互补,两直线平行可得当∠B+∠EAB=180°时,DE∥BC.
解答:解:(1)∵∠B=∠DAB,
∴DE∥BC(内错角相等,两直线平行);
(2)∵∠B+∠EAB=180°,
∴DE∥BC(同旁内角互补,两直线平行).
∴DE∥BC(内错角相等,两直线平行);
(2)∵∠B+∠EAB=180°,
∴DE∥BC(同旁内角互补,两直线平行).
点评:此题主要考查了平行线的判定,关键是掌握平行线的判定定理.同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
相关题目
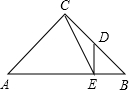 如图,△ABC是等腰三角形,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为E,连接CE,求sin∠ACE的值.
如图,△ABC是等腰三角形,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为E,连接CE,求sin∠ACE的值. 如图,D是等腰三角形的底边BC上的一动点(不与B、C重合),过D作DE∥AB交AC于E,过D作DF∥AC交AB于F,BC=12,BC边上的高AG=8,试说明四边形AEDF的周长不因D的运动而变化.
如图,D是等腰三角形的底边BC上的一动点(不与B、C重合),过D作DE∥AB交AC于E,过D作DF∥AC交AB于F,BC=12,BC边上的高AG=8,试说明四边形AEDF的周长不因D的运动而变化. 如图,DE是过三角形ABC的顶点A的直线.
如图,DE是过三角形ABC的顶点A的直线.