题目内容
 如图,⊙01和⊙02是等圆,半径为1cm,相交于A、B,⊙01经过⊙02的圆心02,连接A01、A02、B01、B02,则图中阴影部分的面积是________cm2.
如图,⊙01和⊙02是等圆,半径为1cm,相交于A、B,⊙01经过⊙02的圆心02,连接A01、A02、B01、B02,则图中阴影部分的面积是________cm2.
( π-
π- )
)
分析:首先计算其中的弓形O1A的面积,利用扇形的面积减去等边三角形的面积即可.
解答:根据题意,得
等边三角形AO1O2的边长是1,根据等边三角形的性质,知它的高是 ,则其面积是
,则其面积是 ;
;
根据扇形的面积公式,得扇形O2O1A的面积是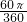 =
= ;
;
则阴影部分的面积是4( -
- )=(
)=( π-
π- )cm2.
)cm2.
故答案为:( π-
π- ).
).
点评:此题考查了弓形面积的求法、扇形的面积公式以及等边三角形的面积.等边三角形的面积等于 ×边长的平方.
×边长的平方.
 π-
π- )
)分析:首先计算其中的弓形O1A的面积,利用扇形的面积减去等边三角形的面积即可.
解答:根据题意,得
等边三角形AO1O2的边长是1,根据等边三角形的性质,知它的高是
 ,则其面积是
,则其面积是 ;
;根据扇形的面积公式,得扇形O2O1A的面积是
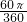 =
= ;
;则阴影部分的面积是4(
 -
- )=(
)=( π-
π- )cm2.
)cm2.故答案为:(
 π-
π- ).
).点评:此题考查了弓形面积的求法、扇形的面积公式以及等边三角形的面积.等边三角形的面积等于
 ×边长的平方.
×边长的平方. 
练习册系列答案
相关题目
 如图,⊙01和⊙02是等圆,半径为1cm,相交于A、B,⊙01经过⊙02的圆心02,连接A01、A02、B01、B02,则图中阴影部分的面积是
如图,⊙01和⊙02是等圆,半径为1cm,相交于A、B,⊙01经过⊙02的圆心02,连接A01、A02、B01、B02,则图中阴影部分的面积是

