题目内容
【题目】某便利店的咖啡单价为10元/杯,为了吸引顾客,该店共推出了三种会员卡,如下表:
会员卡类型 | 办卡费用/元 | 有效期 | 优惠方式 |
A类 | 40 | 1年 | 每杯打九折 |
B类 | 80 | 1年 | 每杯打八折 |
C类 | 130 | 1年 | 一次性购买2杯,第二杯半价 |
例如,购买A类会员卡,1年内购买50次咖啡,每次购买2杯,则消费![]() 元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为( )
元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为( )
A.购买A类会员卡B.购买B类会员卡
C.购买C类会员卡D.不购买会员卡
【答案】C
【解析】
设一年内在该便利店买咖啡的次数为x次,消费的钱数为y元,根据题意得:列出3类会员卡用含x的关系表示消费的费用y,再确定y的范围,进行比较即可解答.
设一年内在该便利店买咖啡的次数为x次,消费的钱数为y元,根据题意得:yA=40+0.9![]() x=40+18x,yB=80+0.8
x=40+18x,yB=80+0.8![]() x=80+16x,yC=130+15
x=80+16x,yC=130+15![]() =130+15x,
=130+15x,
当75≤x≤85时,
1390≤yA≤1570;
1280≤yB≤1440;
1255≤yC≤1405;
由此可见,C类会员年卡消费最低,所以最省钱的方式为购买C类会员年卡.
故选:C.

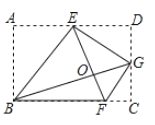
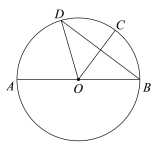
【题目】如图,![]() 是半圆的直径,P是半圆与直径
是半圆的直径,P是半圆与直径![]() 所围成的图形的外部的一定点,D是直径
所围成的图形的外部的一定点,D是直径![]() 上一动点,连接
上一动点,连接![]() 并延长,交半圆于点C,连接
并延长,交半圆于点C,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 两点之间的距离为
两点之间的距离为![]() 两点之间的距离为
两点之间的距离为![]() .
.
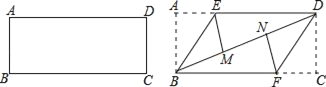
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了探究.
随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表自变量x的值进行取点、画图、测量,分别得到![]() 与x的几组对应值;
与x的几组对应值;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0.47 | 1.31 | 5.02 | 5.91 | 6 | |
| 6 | 5.98 | 5.86 | 5.26 | 3.29 | 1.06 | 0 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;
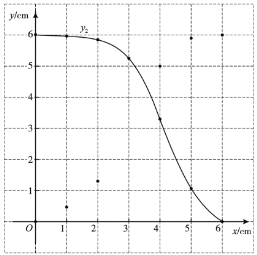
(3)结合函数图象,解决问题:当![]() 有一个角的正弦值为
有一个角的正弦值为![]() 时,
时,![]() 的长约为_____cm.
的长约为_____cm.