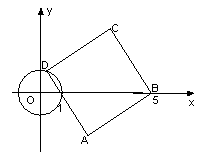
题目内容
如图,⊙ 的半径为
的半径为 ,正方形
,正方形 顶点
顶点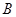 坐标为
坐标为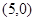 ,顶点
,顶点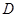 在⊙
在⊙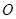 上运动.
上运动.
(1)当点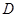 运动到与点
运动到与点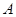 、
、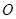 在同一条直线上时,试证明直线
在同一条直线上时,试证明直线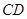 与⊙
与⊙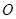 相切;
相切;
(2)当直线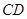 与⊙
与⊙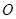 相切时,求
相切时,求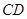 所在直线对应的函数关系式;
所在直线对应的函数关系式;
(3)设点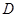 的横坐标为
的横坐标为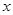 ,正方形
,正方形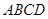 的面积为
的面积为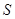 ,求
,求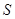 与
与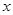 之间的函数关系式,并求出
之间的函数关系式,并求出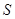 的最大值与最小值.
的最大值与最小值.
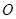 的半径为
的半径为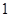 ,正方形
,正方形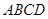 顶点
顶点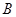 坐标为
坐标为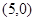 ,顶点
,顶点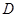 在⊙
在⊙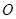 上运动.
上运动.(1)当点
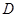 运动到与点
运动到与点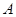 、
、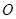 在同一条直线上时,试证明直线
在同一条直线上时,试证明直线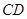 与⊙
与⊙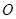 相切;
相切;(2)当直线
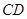 与⊙
与⊙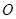 相切时,求
相切时,求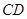 所在直线对应的函数关系式;
所在直线对应的函数关系式;(3)设点
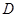 的横坐标为
的横坐标为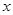 ,正方形
,正方形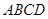 的面积为
的面积为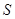 ,求
,求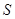 与
与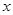 之间的函数关系式,并求出
之间的函数关系式,并求出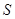 的最大值与最小值.
的最大值与最小值.
(1)证明见解析;(2)y=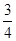 x+
x+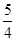 或y=
或y=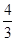 x-
x-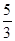 ;(3)S=13-5x,18,8.
;(3)S=13-5x,18,8.
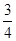 x+
x+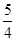 或y=
或y=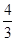 x-
x-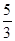 ;(3)S=13-5x,18,8.
;(3)S=13-5x,18,8.试题分析:(1)易得∠ODC=90°,且CD与圆相交于点D,故直线CD与⊙O相切;
(2)分两种情况,①D1点在第二象限时,②D2点在第四象限时,再根据相似三角形的性质,可得比例关系式,代入数据可得CD所在直线对应的函数关系;
(3)设D(x,y0),有S=
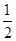 BD2=(26-10x)=13-5x;再根据x的范围可得面积的最大最小值.
BD2=(26-10x)=13-5x;再根据x的范围可得面积的最大最小值.(1)证明:∵四边形ABCD为正方形,
∴AD⊥CD,
∵A、O、D在同一条直线上,
∴∠ODC=90°,
∴直线CD与⊙O相切.
(2)解:直线CD与⊙O相切分两种情况:
①如图1,
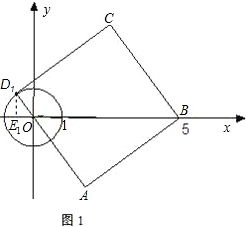
设D1点在第二象限时,
过D1作D1E1⊥x轴于点E1,设此时的正方形的边长为a,
∴(a-1)2+a2=52,
∴a=4或a=-3(舍去),
∵Rt△BOA∽Rt△D1OE1
∴
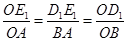 ,
,∴OE1=
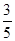 ,D1E1=
,D1E1=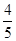 ,
,∴D1(?
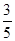 ,
,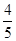 ).
).∴直线OD的函数关系式为y=?
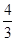 x.
x.∵AD1⊥CD1,
∴设直线CD1的解析式为y=
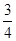 x+b,
x+b,把D1(?
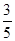 ,
,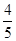 )代入解析式得b=
)代入解析式得b=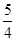 ;
;∴函数解析式为y=
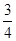 x+
x+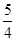 .
.②如图2,
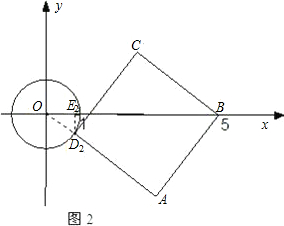
设D2点在第四象限时,过D2作D2E2⊥x轴于点E2,
设此时的正方形的边长为b,则(b+1)2+b2=52,
解得b=3或b=-4(舍去).
∵Rt△BOA∽Rt△D2OE2,
∴
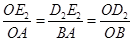 ,
,∴OE2=
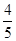 ,D2E2=
,D2E2=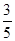 ,
,∴D2(
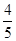 ,?
,?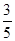 ),
),∴直线OD的函数关系式为y=?
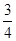 x.
x.∵AD2⊥CD2,
∴设直线CD2的解析式为y=
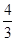 x+b,
x+b,把D2(
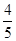 ,?
,?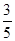 )代入解析式得b=-
)代入解析式得b=-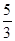 ;
;∴函数解析式为y=
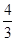 x-
x-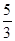 .
.(3)解:设D(x,y0),
∴y0=±
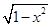 ,
,∵B(5,0),
∴BD2=(5-x)2+(1-x2)=26-10x,
∴S=
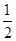 BD2=
BD2=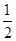 (26-10x)=13-5x,
(26-10x)=13-5x,∵-1≤x≤1,
∴S最大值=13+5=18,S最小值=13-5=8.

练习册系列答案
相关题目
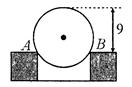
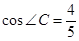 ,DF=9,求⊙O的半径。
,DF=9,求⊙O的半径。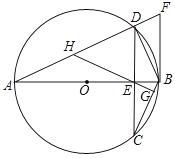
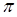
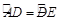 ,AB=5,BD=4,则sin∠ECB= .
,AB=5,BD=4,则sin∠ECB= .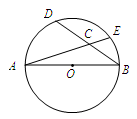
 的中点,∠ABC=50°,则∠DAB等于( )
的中点,∠ABC=50°,则∠DAB等于( )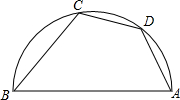
 的直径,AB=10,C是⊙
的直径,AB=10,C是⊙