Question

已知等腰△ABC的底边BC=8，腰长AB=5，一动点P在底边上从点B开始向点C以每秒0.5的速度运动，当点P运动到PA与腰垂直的位置时，点P运动的时间应为

3.5或12.5

秒．

Answer 1

分析：根据等腰三角形三线合一性质可得到BD的长，由勾股定理可求得AD的长，再分两种情况进行分析：①PA⊥AC②PA⊥AB，从而可得到运动的时间．

解答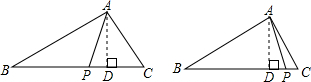：解：如图，作AD⊥BC，交BC于点D，
∵BC=8cm，
∴BD=CD=

1

2

BC=4cm，
∴AD=

AB2-BD2

=3，
分两种情况：当点P运动t秒后有PA⊥AC时，
∵AP²=PD²+AD²=PC²-AC²，∴PD²+AD²=PC²-AC²，
∴PD²+3²=（PD+4）²-5²∴PD=2.25，
∴BP=4-2.25=1.75=0.5t，
∴t=3 5秒，
当点P运动t秒后有PA⊥AB时，同理可证得PD=2.25，
∴BP=4+2.25=6.25=0.5t，
∴t=12.5秒，
∴点P运动的时间为3.5秒或12.5秒．
故答案为：3.5或12.5．

点评：本题考查了等腰三角形的性质和勾股定理的应用，在解题时还要注意分类讨论思想的运用．