题目内容
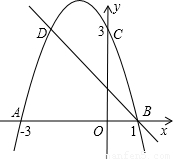
如图，二次函数的对称轴是直线x=1，它与y轴交于点（0，3），与x轴交于点A、B，并且已知该二次函数有最小值y=-4．（1）求该二次函数的解析式；
（2）求点A与点B之间的距离；
（3）将该抛物线沿x轴平移几个单位，可使平移后所得图象经过坐标原点？并写出平移后所得图象与x轴的另一个交点的坐标．
分析：（1）利用已知得出二次函数的顶点坐标即可利用顶点式求出二次函数解析式；
（2）利用二次函数图象与x轴交点求法，y=0，求出x即可，再利用两点距离公式求出即可；
（3）根据（2）中AB的长度，以及图象经过原点，即可得出另一点的坐标．
（2）利用二次函数图象与x轴交点求法，y=0，求出x即可，再利用两点距离公式求出即可；
（3）根据（2）中AB的长度，以及图象经过原点，即可得出另一点的坐标．
解答：解：（1）∵二次函数的对称轴是直线x=1，它与y轴交于点（0，3），该二次函数有最小值y=-4．
∴二次函数的顶点坐标为：（1，-4），
代入顶点式方程得：y=a（x-1）2-4，
将（0，3）代入上式得出：3=a（0-1）2-4，
解得：a=7，
∴二次函数的解析式为：y=7（x-1）2-4，
（2）∵二次函数图象与x轴交于点A、B，
∴0=7（x-1）2-4，
解得：x1=1+
，x2=1-
；
∴AB=1+
-（1-
）=
；
（3）根据函数图象与x轴的交点坐标即可得出，图象向右平移1-
个单位长度或向左平移1+
个单位长度时，图象过原点，
∴根据AB=1+
-（1-
）=
；
∴平移后所得图象与x轴的另一个交点的坐标为：（-
，0）或（
，0）．
∴二次函数的顶点坐标为：（1，-4），
代入顶点式方程得：y=a（x-1）2-4，
将（0，3）代入上式得出：3=a（0-1）2-4，
解得：a=7，
∴二次函数的解析式为：y=7（x-1）2-4，
（2）∵二次函数图象与x轴交于点A、B，
∴0=7（x-1）2-4，
解得：x1=1+
2
| ||
| 7 |
2
| ||
| 7 |
∴AB=1+
2
| ||
| 7 |
2
| ||
| 7 |
4
| ||
| 7 |
（3）根据函数图象与x轴的交点坐标即可得出，图象向右平移1-
2
| ||
| 7 |
2
| ||
| 7 |
∴根据AB=1+
2
| ||
| 7 |
2
| ||
| 7 |
4
| ||
| 7 |
∴平移后所得图象与x轴的另一个交点的坐标为：（-
4
| ||
| 7 |
4
| ||
| 7 |
点评：此题主要考查了顶点式求二次函数解析式以及二次函数与x轴交点坐标求法和二次函数图象的平移等知识，此题比较基础，根据图象平移的性质，图象大小不发生变化得出图象与x轴的交点距离不变是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
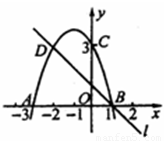
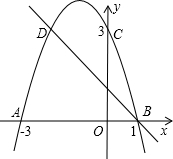0，3），点C、D是二次函数图象上的一对对称点．一次函的图象过点B、D．
