题目内容
 如图,△ABC为等边三角形,其边长为6,将它沿BC边上的高AD剪成两个全等的直角三角形,用这两个全等的直角三角形拼平行四边形.
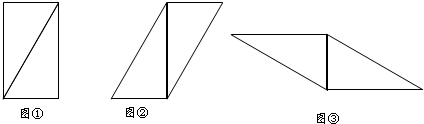
如图,△ABC为等边三角形,其边长为6,将它沿BC边上的高AD剪成两个全等的直角三角形,用这两个全等的直角三角形拼平行四边形.(1)画出所有可以拼成的不同的平行四边形;
(2)求出上面拼成的平行四边形的对角线长.
分析:(1)例如两个直角三角形可以拼成一个矩形,而矩形的对角线相等且可以通过求解直角三角形得出,两条短直角边重合又是一种情况,
(2)不同的拼法,对角线的长度也不同,答案并不唯一.对角线的长度都可以通过作直角三角形求解得出.
(2)不同的拼法,对角线的长度也不同,答案并不唯一.对角线的长度都可以通过作直角三角形求解得出.
解答:解:(1)共可拼成以下三种不同的情况.
(2)在等边△ABC中,
∵AD⊥BC,
∴BD=
BC=3,
∴在Rt△ABD中,AD=
=
…(4分)
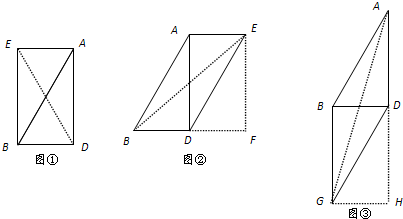
①如图①,连接ED,则∠EBD=∠EBA+∠ABD=90°
∴∠EBD=∠ADB
又∵BE=AD,BD=BD
∴△EBD≌△ADB
∴ED=AB=3,
即:两条对角线的长都是3.…(5分)
②如图②,连接BE,过点E作EF垂直BD的延长线于点F,
则EF=AD=
,DF=AE=3.
在Rt△BEF中:BE=
=
即:两条对角线的长分别为3、
.…(7分)
③如图③,连接AG,过点G作GH垂直AD的延长线于点H,
则GH=BD=3,DH=BG=AD=
所以AH=AD+DH=2
在Rt△AHG中:AG=
=
即:两条对角线的长分别为3、
.…(9分)


(2)在等边△ABC中,
∵AD⊥BC,
∴BD=
| 1 |
| 2 |
∴在Rt△ABD中,AD=
| AB2-BD2 |
| 27 |
①如图①,连接ED,则∠EBD=∠EBA+∠ABD=90°
∴∠EBD=∠ADB
又∵BE=AD,BD=BD
∴△EBD≌△ADB
∴ED=AB=3,
即:两条对角线的长都是3.…(5分)
②如图②,连接BE,过点E作EF垂直BD的延长线于点F,
则EF=AD=
| 27 |
在Rt△BEF中:BE=
| BF2+EF2 |
| 63 |
即:两条对角线的长分别为3、
| 63 |
③如图③,连接AG,过点G作GH垂直AD的延长线于点H,
则GH=BD=3,DH=BG=AD=
| 27 |
所以AH=AD+DH=2
| 27 |
在Rt△AHG中:AG=
| AH2+GH2 |
| 117 |
即:两条对角线的长分别为3、
| 117 |
点评:本题主要考查平行四边形的判定及全等三角形的判定,性质和等边三角形的性质问题,能够画出正确的图形,并作简单的计算.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=
16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=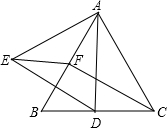 如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE. 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1 如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为一边作等边三角形ADE.
如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为一边作等边三角形ADE. 如图,△ABC为等边△,EC=ED,∠CED=120゜,P为BD的中点,求证:AE=2PE.
如图,△ABC为等边△,EC=ED,∠CED=120゜,P为BD的中点,求证:AE=2PE.