题目内容
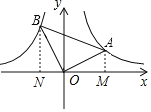
【题目】如图，∠AOB＝90°，且OA，OB分别与反比例函数y＝
（x＞0）、y＝﹣
（x＜0）的图象交于A，B两点，则sin∠OAB的值是（ ）
A.
B.
C.
D.
【答案】B
【解析】
根据反比例函数的几何意义，可求出△AOM，△BON的面积，由于∠AOB＝90°，可证出△AOM∽△BON，由相似三角形的面积比等于相似比的平方，进而求出相似比，即直角三角形AOB两条直角边的比，可求出斜边，进而求sin∠OAB
过点A、B分别作AM⊥x轴，BN⊥x轴，垂足为M、N，
∵点A在反比例函数y＝
（x＞0）的图象上，
∴S△AOM＝
×3＝
，
∵点B在反比例函数y＝﹣
（x＜0）的图象上，
∴S△BON＝×4＝2，
∵∠AOB＝90°
∴△BON∽△AOM，
∴（
）2＝
＝
，
∴
＝
，
在Rt△AOB中，设OB＝2m，则OA＝
m，
∴AB＝
＝
m，
∴sin∠OAB＝
＝
＝
，
故选：B．
练习册系列答案
名校课堂系列答案
相关题目
