题目内容
如图所示，某公园入口处原有三级台阶，每级台阶高20cm，宽30cm．为方便残疾人士，拟将台阶改为斜坡．现台阶的起点为A，斜坡的起始点为C，若将坡角∠BCA设计为30°，则AC的长度应为（ ）
A、60
| ||
B、60(
| ||
| C、60cm | ||
D、60(
|
考点：解直角三角形的应用-坡度坡角问题
专题：
分析：首先过点B作BD⊥AC于D，根据题意即可求得AD与BD的长，然后由坡角∠BCA=30°，求得CD的长，继而求得答案．
解答：
解：过点B作BD⊥AC于D，
根据题意得：AD=2×30=60cm，BD=20×3=60cm，
∵坡角∠BCA=30°，
∴BD：CD=1：
，
∴CD=
BD=
×60=60
cm，
∴AC=CD-AD=60
-60=60（
-1）cm．
故选B．
解：过点B作BD⊥AC于D，根据题意得：AD=2×30=60cm，BD=20×3=60cm，
∵坡角∠BCA=30°，
∴BD：CD=1：
| 3 |
∴CD=
| 3 |
| 3 |
| 3 |
∴AC=CD-AD=60
| 3 |
| 3 |
故选B．
点评：此题考查了解直角三角形的应用：坡度问题．此题难度适中，注意掌握坡度的定义，注意数形结合思想的应用与辅助线的作法．
练习册系列答案
相关题目
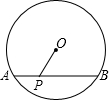如图，⊙O的直径为10，弦AB的长为8，P为弦AB上不同于A，B的一点．若OP的长为整数，则满足条件的点P有（ ）| A、2个 | B、3个 | C、4个 | D、5个 |
下列说法中，不正确的是（ ）
| A、圆是轴对称图形 |
| B、圆的任意一条直径所在的直线都是圆的对称轴 |
| C、圆的任一直径都是圆的对称轴 |
| D、经过圆心的任意直线都是圆的对称轴 |
如图，一枚半径为r的硬币沿着直线滚动一圈，圆心经过的距离是（ ）| A、4πr | B、2πr |
| C、πr | D、2r |
式子-□•（3a2b）=12a5b2c成立时，□内应填上（ ）
| A、4a3bc |
| B、36a3bc |
| C、-4a3bc |
| D、-36a3bc |
若抛物线y=(3+m)xm2-10的开口向下，则m的值为（ ）
A、2
| ||
B、-2
| ||
| C、3 | ||
| D、-3 |
下列式子从左到右的变形中，错误的是（ ）
| A、9x2=（3x）2 |
| B、4x4=（2x2）2 |
| C、-0.25y4=-（0.5y2）2 |
| D、-16x2y4=（-4xy2）2 |