题目内容
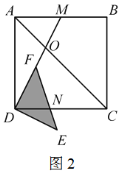
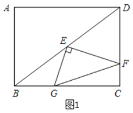
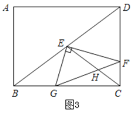
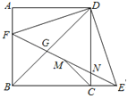
【题目】如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连结EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DE=DF;②∠CME=∠CDE;③DG2=GN GE;④若BF=2,![]() 则正确的结论有( )个.
则正确的结论有( )个.
A.4B.3C.2D.1
【答案】A
【解析】
①根据正方形的性质可证明![]() ,则可判断①正误;
,则可判断①正误;
②首先利用![]() 和直角三角形斜边中线的性质得出
和直角三角形斜边中线的性质得出![]() ,然后利用三角形外角的性质和直角三角形两锐角互余即可判断;
,然后利用三角形外角的性质和直角三角形两锐角互余即可判断;
③首先证明![]() ,则有
,则有![]() ,即可判断③的正误;
,即可判断③的正误;
④首先利用平行线分线段成比例求出MH的长度,然后解直角三角形即可求出MC的长度,由此可判断④的正误.
∵四边形ABCD是正方形,
∴![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,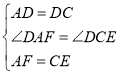
![]() ,
,
![]() ,故①正确;
,故①正确;
连接DM,BM,
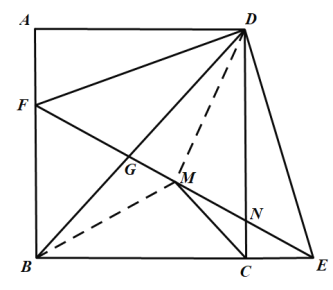
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
∵点M是EF的中点,
∴![]() .
.
![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,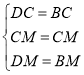
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,故②正确;
,故②正确;
∵![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,故③正确;
,故③正确;
过点M作![]() 交BC于H,
交BC于H,
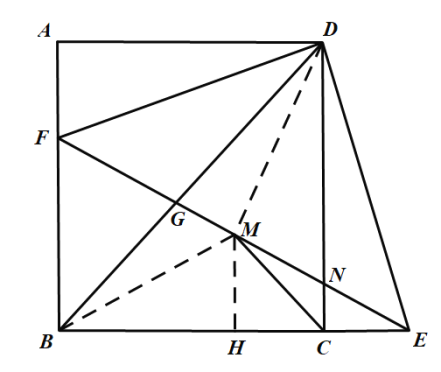
![]() ,
,
![]() ,
,
∴![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,故④正确;
,故④正确;
∴正确的有:①②③④,
故选:A.

练习册系列答案
相关题目