题目内容
已知在△ABC中,AB=AC,∠BAC=90°,∠CAD=60°,BD=BC,AB=1,求AD的长.
考点:等腰直角三角形
专题:
分析:根据题意画出图形,有两种情况:
①当∠CAD在∠BAC的外部,如图(1),延长BA,过D作DE⊥AB,垂足为E,可得∠DAE=30°,设DE=x,根据30°角所对的直角边等于斜边的一半,可得AD=2x,由勾股定理得AE=
x,然后在Rt△BED中,由勾股定理可求x=
,进而求出AD=
;
②当∠CAD在∠BAC的内部,如图(2),过点B作BF⊥AD,垂足为F,由∠BAC=90°,∠CAD=60°,可得∠BAD=30°,在Rt△ABF中,根据30°角所对的直角边等于斜边的一半,可得BF=
AB=
,然后由勾股定理可求AF=
,然后在Rt△BDF中,由勾股定理可求DF=
,所以AD=AF+DF=
.
①当∠CAD在∠BAC的外部,如图(1),延长BA,过D作DE⊥AB,垂足为E,可得∠DAE=30°,设DE=x,根据30°角所对的直角边等于斜边的一半,可得AD=2x,由勾股定理得AE=
| 3 |
-
| ||||
| 4 |
-
| ||||
| 2 |
②当∠CAD在∠BAC的内部,如图(2),过点B作BF⊥AD,垂足为F,由∠BAC=90°,∠CAD=60°,可得∠BAD=30°,在Rt△ABF中,根据30°角所对的直角边等于斜边的一半,可得BF=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||||
| 2 |
解答:解:①当∠CAD在∠BAC的外部,如图(1),
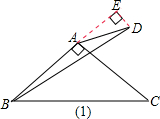
延长BA,过D作DE⊥AB,垂足为E,
∵∠BAC=90°,∠CAD=60°,
∴∠DAE=30°,
设DE=x,则AD=2x,
由勾股定理得:AE=
x,
△ABC中中,
∵AB=AC,∠BAC=90°,AB=1,
∴AC=1,
由勾股定理得:
AB2+AC2=BC2,
即:12+12=BC2,
∴BC=
,
∵BD=BC,
∴BD=
,
在Rt△BED中,由勾股定理得:
BE2+ED2=BD2,
即:(1+
x)2+x2=(
)2,
解:x1=
,x2=
(舍去),
∴AD=2x=
;
②当∠CAD在∠BAC的内部,如图(2),
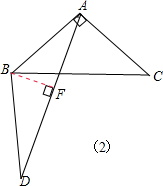
过点B作BF⊥AD,垂足为F,
∵∠BAC=90°,∠CAD=60°,
∴∠BAD=30°,
∴BF=
AB=
,
在Rt△ABF中,
由勾股定理得:
AB2=BF2+AF2,
即:12=(
)2+AF2,
∴AF=
,
∵AB=AC,∠BAC=90°,AB=1,
∴AC=1,
由勾股定理得:
AB2+AC2=BC2,
即:12+12=BC2,
∴BC=
,
∵BD=BC,
∴BD=
,
在Rt△BED中,由勾股定理得:
BF2+FD2=BD2,
即:(
)2+FD2=(
)2,
∴DF=
,
∴AD=AF+DF=
.

延长BA,过D作DE⊥AB,垂足为E,
∵∠BAC=90°,∠CAD=60°,
∴∠DAE=30°,
设DE=x,则AD=2x,
由勾股定理得:AE=
| 3 |
△ABC中中,
∵AB=AC,∠BAC=90°,AB=1,
∴AC=1,
由勾股定理得:
AB2+AC2=BC2,
即:12+12=BC2,
∴BC=
| 2 |
∵BD=BC,
∴BD=
| 2 |
在Rt△BED中,由勾股定理得:
BE2+ED2=BD2,
即:(1+
| 3 |
| 2 |
解:x1=
-
| ||||
| 4 |
-
| ||||
| 4 |
∴AD=2x=
-
| ||||
| 2 |
②当∠CAD在∠BAC的内部,如图(2),

过点B作BF⊥AD,垂足为F,
∵∠BAC=90°,∠CAD=60°,
∴∠BAD=30°,
∴BF=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ABF中,
由勾股定理得:
AB2=BF2+AF2,
即:12=(
| 1 |
| 2 |
∴AF=
| ||
| 2 |
∵AB=AC,∠BAC=90°,AB=1,
∴AC=1,
由勾股定理得:
AB2+AC2=BC2,
即:12+12=BC2,
∴BC=
| 2 |
∵BD=BC,
∴BD=
| 2 |
在Rt△BED中,由勾股定理得:
BF2+FD2=BD2,
即:(
| 1 |
| 2 |
| 2 |
∴DF=
| ||
| 2 |
∴AD=AF+DF=
| ||||
| 2 |
点评:此题考查了等腰直角三角形的性质,解题的关键是:根据题意画出图形,分两种情况:①当∠CAD在∠BAC的外部,②当∠CAD在∠BAC的内部.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
将4.34059精确到千分位是( )
| A、4.341 |
| B、4.34 |
| C、4.3406 |
| D、4.340 |
 如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠2=20°,则∠1=
如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠2=20°,则∠1=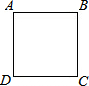 如图,沿着边长为90cm的正方形,按照A-B-C-D-A…的方向,电子蚂蚁甲从A以65cm/min的速度前进,电子蚂蚁乙同时从A以72cm/min的速度前进.
如图,沿着边长为90cm的正方形,按照A-B-C-D-A…的方向,电子蚂蚁甲从A以65cm/min的速度前进,电子蚂蚁乙同时从A以72cm/min的速度前进.