题目内容
20.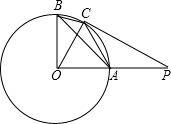 如图,已知BO⊥PO,AB是⊙O上弦,点C是⊙O上的动点,∠CBA=∠ACP.
如图,已知BO⊥PO,AB是⊙O上弦,点C是⊙O上的动点,∠CBA=∠ACP.(1)求证:PC与⊙O相切;
(2)若点A是PO的中点,⊙O的半径是2,求四边形OACB的面积.
分析 (1)先求得∠OAC=∠OCA,从而根据三角形内角和定理得出2∠OCA+∠AOC=180°,进而得出$∠OCA+\frac{1}{2}∠AOC$=90°,由∠CBA=∠ACP,$∠CBA=\frac{1}{2}∠AOC$,得出∠OCA+∠ACP=90°,即可证得结论;
(2)根据已知求得三角形AOC是等边三角形,进而得出∠BOC=30°,作CD⊥OP,BE⊥OC,通过解直角三角形求得CD、BE,然后根据S四边形OACB=S△AOC+S△BOC即可求得.
解答 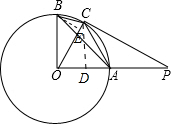 解:(1)∵OA=OC,
解:(1)∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OCA+∠AOC=180°,
∴2∠OCA+∠AOC=180°,
∴$∠OCA+\frac{1}{2}∠AOC$=90°,
∵∠CBA=∠ACP,$∠CBA=\frac{1}{2}∠AOC$,
∴∠OCA+∠ACP=90°,
∴OC⊥PC,
∴PC与⊙O相切;
(2)∵∠PCO=90°,点A是PO的中点,
∴AC=OC=PA,
∵OC=OA,
∴△AOC是等边三角形,
∴∠AOC=60°,
∵BO⊥PO,
∴∠BOC=30°,
作CD⊥OP,BE⊥OC,
∴CD=$\frac{\sqrt{3}}{2}$OC=$\sqrt{3}$,BE=$\frac{1}{2}$OB=1,
∴S四边形OACB=S△AOC+S△BOC=$\frac{1}{2}$OA•CD+$\frac{1}{2}$OC•BE=$\frac{1}{2}$×2×$\sqrt{3}$+$\frac{1}{2}$×2×1=$\sqrt{3}$+1.
点评 本题考查了三角形的内角和定理,切线的判定,等边三角形的判定和性质,解直角三角形等,作出辅助线,求得三角形的高CD、BE是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目

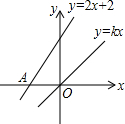 如图,直线y=2x+2与x轴交于点A,与y轴交于点B,点P为正比例函数y=kx(k>0)的图象上一点,且S△AOP:S△BOP=1:2,求k的值.
如图,直线y=2x+2与x轴交于点A,与y轴交于点B,点P为正比例函数y=kx(k>0)的图象上一点,且S△AOP:S△BOP=1:2,求k的值.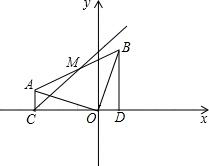 在平面直角坐标系中,∠ACO=90°.把AO绕O点顺时针旋转90°得OB,连接AB,作BD⊥x轴于D,点A的坐标为(-3,1).
在平面直角坐标系中,∠ACO=90°.把AO绕O点顺时针旋转90°得OB,连接AB,作BD⊥x轴于D,点A的坐标为(-3,1). 如图,在一张长为5,宽为4的矩形纸片上,现要剪下一个腰长为3的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为$\frac{9}{2}$或2$\sqrt{2}$或$\frac{3}{2}$$\sqrt{5}$.
如图,在一张长为5,宽为4的矩形纸片上,现要剪下一个腰长为3的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为$\frac{9}{2}$或2$\sqrt{2}$或$\frac{3}{2}$$\sqrt{5}$.