题目内容

在关于x的方程x²-2ax+ $数学公式$ b²=0中，a，b分别是一个面积为12的等腰三角形的腰与底边的长，且这个方程的两根之差的绝对值为8．则这个三角形的内切圆面积是________．

$\text{[math]}$
分析：先根据一元二次方程的根与系数的关系知：x₁+x₂=2a，x₁x₂= $\text{[math]}$ b²，利用（x₁+x₂）²-4x₁x₂=64可列方程4a²-b²=64；再根据a，b分别是一个面积为12的等腰三角形的腰与底边的长，可得到S_△= $\text{[math]}$ b× $\text{[math]}$ × $\text{[math]}$ =12，与4a²-b²=64联立方程即可解得b，a的值；再设内切圆半径为x，利用AD²+DF²=AF²=（AE-EF）²，列方程2²+x²=（4-x）²，解得半径x，代入三角形的内切圆面积公式即可求解．
解答：

解：如图，AB=AC=a，BC=b，AE⊥BC，FD⊥AB，圆F是△ABC的内切圆，
∴BE= $\text{[math]}$ BC= $\text{[math]}$ b，AE= $\text{[math]}$ = $\text{[math]}$ $\text{[math]}$ ；
∵x₁+x₂=2a，x₁x₂= $\text{[math]}$ b²，
又∵|x₁-x₂|=8，
∴（x₁+x₂）²-4x₁x₂=64，即4a²-b²=64；
∵a，b分别是一个面积为12的等腰三角形的腰与底边的长，
∴S_△= $\text{[math]}$ b× $\text{[math]}$ × $\text{[math]}$ =12，
与4a²-b²=64联立方程解得，b=6，a=5；
设内切圆半径为x，则
EF=DF=x，
∴BE=BD=3，AD=AB-BD=5-3=2，AD²+DF²=AF²=（AE-EF）²，
∴2²+x²=（4-x）²，
解得x= $\text{[math]}$ ；
∴三角形的内切圆面积=π×（ $\text{[math]}$ ）²= $\text{[math]}$ ．
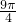点评：主要考查：等腰三角形的三线合一，三角形内切圆的意义，直角三角形的性质、勾股定理、根与系数的关系．此题难点在于利用根与系数的关系和勾股定理求a，b的值．学生丢分率较高．