题目内容
19．已知am+2n=4，a3n=8．求am-n的值．分析 根据同底数幂的除法法则计算即可．
解答 解：∵am+2n÷a3n=4÷8=$\frac{1}{2}$，
∴am-n=$\frac{1}{2}$．
点评 本题考查的是同底数幂的除法，掌握同底数幂的除法法则：底数不变，指数相减是解题的关键．
练习册系列答案
相关题目
9．下列方程中，是一元二次方程的是（ ）
| A． | x+2y=1 | B． | 7x+5=6（x-1） | C． | x2-4x=3 | D． | $\frac{1}{x}$-2=x |
将正整数按如下规律排列，若2016在第n行第m列，则n=672，m=2．
11．下列分式的变形不正确的是（ ）
| A． | $\frac{-（a+b）}{c}$=-$\frac{a+b}{c}$ | B． | $\frac{-a+b}{c}$=-$\frac{a+b}{c}$ | C． | $\frac{-a-b}{c}$=-$\frac{a+b}{c}$ | D． | $\frac{b-a}{-c}$=$\frac{a-b}{c}$ |
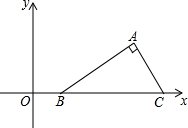在平面直角坐标系中，Rt△ABC的斜边BC在x轴上，点B的坐标为（1，0），AC=2，∠ABC=30°，把Rt△ABC先绕点B顺时针旋转180°，然后向下平移2个单位，则点A的对应点D的坐标为（-2，-2-$\sqrt{3}$）．
1．下列计算正确的是（ ）
| A． | a3•a2=a6 | B． | （-2a2）3=-8a6 | C． | （a+b）2=a2+b2 | D． | 2a+3a=5a2 |