题目内容
【题目】如图,已知点![]() 满足
满足![]() .将线段
.将线段![]() 先向上平移2个单位,再向右平移1个单位后得到线段
先向上平移2个单位,再向右平移1个单位后得到线段![]() ,并连接
,并连接![]() .
.

(1)请求出点![]() 和点
和点![]() 的坐标;
的坐标;
(2)点![]() 从
从![]() 点出发,以每秒1个单位的速度向上平移运动.设运动时间为
点出发,以每秒1个单位的速度向上平移运动.设运动时间为![]() 秒,问:是否存在这样的
秒,问:是否存在这样的![]() ,使得四边形
,使得四边形![]() 的面积等于8?若存在,请求出
的面积等于8?若存在,请求出![]() 的值:若不存在,请说明理由;
的值:若不存在,请说明理由;
(3)在(2)的条件下,点![]() 从
从![]() 点出发的同时,点
点出发的同时,点![]() 从点
从点![]() 出发,以每秒2个单位的速度向左平移运动,设射线
出发,以每秒2个单位的速度向左平移运动,设射线![]() 交
交![]() 轴于点
轴于点![]() .设运动时间为
.设运动时间为![]() 秒,问:
秒,问:![]() 的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由.
【答案】(1)(-1,0)、(3,0);(2)存在,t=![]() ;(3)不变,理由见解析.
;(3)不变,理由见解析.
【解析】
(1)根据非负性求得a、b,即可确定点![]() 和点
和点![]() 的坐标;
的坐标;
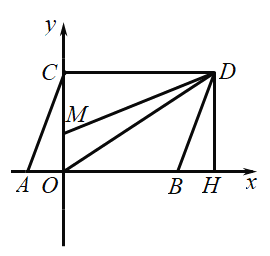
(2)过D作DH⊥OB的延长线,垂足为H;先确定点C和点D的坐标;进而确定OB、DC、DH的长;设D点坐标为(0,t),连接MD、OD,则四边形![]() 的面积等于三角形OBD的面积加上三角形OMD的面积等于8,然后解出t即可.
的面积等于三角形OBD的面积加上三角形OMD的面积等于8,然后解出t即可.
(3)设运动时间为![]() 秒,OM=t、ON=3-2t;过D作DH⊥OB的延长线,垂足为H,连接OM,OD
秒,OM=t、ON=3-2t;过D作DH⊥OB的延长线,垂足为H,连接OM,OD
.由![]() =S四边形OMDN、S四边形OMDN=S△OND+S△OMD可得
=S四边形OMDN、S四边形OMDN=S△OND+S△OMD可得![]() ,然后求解即可.
,然后求解即可.
解:(1)∵![]()
∴3a+b=0,b-3=0,即a=-1,b=3
∴点![]() 和点
和点![]() 的坐标分别为(-1,0)和(3,0)
的坐标分别为(-1,0)和(3,0)
(2)存在;
过D作DH⊥OB的延长线,垂足为H.
由题意得点C和点D的坐标分别为(0,2)和(4,2)
∴CD=4,DH=2,OB=3
设D点坐标为(0,t),连接MD、OD,
∴OM=t
∵S四边形OMDB=S△OBD+S△OMD=8,
∴![]() ,即
,即![]() ,解得t=
,解得t=![]() ;
;
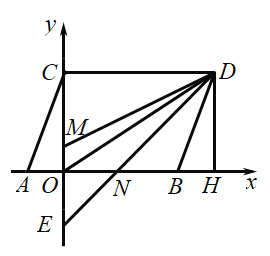
(3)不变,理由如下:
如图:当运动时间为![]() 秒,OM=t,ON=3-2t,
秒,OM=t,ON=3-2t,
过D作DH⊥OB的延长线,垂足为H,连接OM,OD
∵![]() =S四边形OMDN,S四边形OMDN=S△OND+S△OMD
=S四边形OMDN,S四边形OMDN=S△OND+S△OMD
∴![]()
=S△OND+S△OMD
=![]()
=![]()
=3-2t+2t
=3
∴![]() 的值不会变化
的值不会变化

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案




