题目内容
亲爱的同学们,在我们进入高中以后,将还会学到三角函数公式:sin(α+β)=sinαcosβ+cosαsinβ,cos(α+β)=cosαcosβ-sinαsinβ例:sin75°=sin(30°+45°)=sin30° cos45°+cos30° sin45°=

(1)试仿照例题,求出cos75°的准确值;
(2)我们知道:
 ,试求出tan75°的准确值;
,试求出tan75°的准确值;(3)根据所学知识,请你巧妙地构造一个合适的直角三角形,求出tan75°的准确值(要求分母有理化),和(2)中的结论进行比较.
【答案】分析:从题中给出的信息进行答题:
(1)把75°化为30°+45°直接代入三角函数公式:sin(α+β)=sinαcosβ+cosαsinβ,cos(α+β)=cosαcosβ-sinαsinβ计算即可;
(2)把tan75°代入tanα= ,再把(1)及例题中的数值代入即可.
,再把(1)及例题中的数值代入即可.
(3)根据题意画出图形,利用三角函数的定义解答即可.
解答:解:(1)∵cos(α+β)=cosαcosβ-sinαsinβ,
∴cos75°=cos(30°+45°)=cos30°cos45°-sin30°sin 45°,
= ×
× -
- ×
× =
= ;
;
(2)∵ ,
,
∴tan75°= =
= =2+
=2+ ;
;
(3)如下图:tan75°=tan∠CBD= =
= +2.
+2.

点评:本题是信息题,解答此题的关键是:
(1)按照cos(α+β)=cosαcosβ-sinαsinβ求出了cos75°的值;
(2)按照 ,求出了tan75°的准确值;
,求出了tan75°的准确值;
(3)利用三角函数值的定义解答.
(1)把75°化为30°+45°直接代入三角函数公式:sin(α+β)=sinαcosβ+cosαsinβ,cos(α+β)=cosαcosβ-sinαsinβ计算即可;
(2)把tan75°代入tanα=
 ,再把(1)及例题中的数值代入即可.
,再把(1)及例题中的数值代入即可.(3)根据题意画出图形,利用三角函数的定义解答即可.
解答:解:(1)∵cos(α+β)=cosαcosβ-sinαsinβ,
∴cos75°=cos(30°+45°)=cos30°cos45°-sin30°sin 45°,
=
 ×
× -
- ×
× =
= ;
;(2)∵
 ,
,∴tan75°=
 =
= =2+
=2+ ;
;(3)如下图:tan75°=tan∠CBD=
 =
= +2.
+2.
点评:本题是信息题,解答此题的关键是:
(1)按照cos(α+β)=cosαcosβ-sinαsinβ求出了cos75°的值;
(2)按照
 ,求出了tan75°的准确值;
,求出了tan75°的准确值;(3)利用三角函数值的定义解答.

练习册系列答案
相关题目
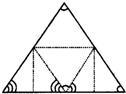 13、亲爱的同学们,在我们的生活中处处有数学的身影,如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于
13、亲爱的同学们,在我们的生活中处处有数学的身影,如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于

