题目内容
△ABC的内角A和B都是锐角,CD是高,若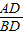 =
=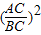 ,则△ABC是( )
,则△ABC是( )A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
【答案】分析:分别从当AD=BD时,可得△ABC是等腰三角形;当AC2=AD•AB,BC2=BD•AB时,△ABC是直角三角形.
解答: 解:①若AD=BD,
解:①若AD=BD,
∵ =
= ,
,
∴AC=BC,
此时CD是高,符合题意,
即△ABC是等腰三角形;
②∵ =
= ,
,
∴ =
= =
= ,
,
∴当AC2=AD•AB,BC2=BD•AB时成立,
即 ,
,
∵∠A是公共角,
∴△ABC∽△ACD,
∴∠ACB=∠ADC=90°,
∴△ABC是直角三角形;
∴△ABC是等腰三角形或直角三角形.
故选D.
点评:此题考查了相似三角形的判定与性质、等腰三角形的判定与性质以及直角三角形的判定.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.
解答:
 解:①若AD=BD,
解:①若AD=BD,∵
 =
= ,
,∴AC=BC,
此时CD是高,符合题意,
即△ABC是等腰三角形;
②∵
 =
= ,
,∴
 =
= =
= ,
,∴当AC2=AD•AB,BC2=BD•AB时成立,
即
 ,
,∵∠A是公共角,
∴△ABC∽△ACD,
∴∠ACB=∠ADC=90°,
∴△ABC是直角三角形;
∴△ABC是等腰三角形或直角三角形.
故选D.
点评:此题考查了相似三角形的判定与性质、等腰三角形的判定与性质以及直角三角形的判定.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目

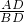 =
= ,则△ABC是
,则△ABC是