题目内容
如图1,△ABC和△ADE都是等腰直角三角形,∠C和∠ADE都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合得到图1,再将图2作为“基本图形”绕着A点经过逆时针连续旋转得到图2.两次旋转的角度分别为

- A.45°,90°
- B.90°,45°
- C.60°,30°
- D.30°,60°
A
分析:图1中可知旋转角是∠EAB,再结合等腰直角三角形的性质,易求∠EAB;图2中是把图1作为基本图形,那么旋转角就是∠FAB,结合等腰直角三角形的性质易求∠FAB.
解答: 解:根据图1可知,
解:根据图1可知,
∵△ABC和△ADE是等腰直角三角形,
∴∠CAB=45°,
即△ABC绕点A逆时针旋转45°可到△ADE;
如右图,
∵△ABC和△ADE是等腰直角三角形,
∴∠DAE=∠CAB=45°,
∴∠FAB=∠DAE+∠CAB=90°,
即图1可以逆时针连续旋转90°得到图2.
故选A.
点评:本题考查了旋转的性质、等腰直角三角形的性质,解题的关键是理解旋转的性质,能找对旋转中心、旋转角.
分析:图1中可知旋转角是∠EAB,再结合等腰直角三角形的性质,易求∠EAB;图2中是把图1作为基本图形,那么旋转角就是∠FAB,结合等腰直角三角形的性质易求∠FAB.
解答:
 解:根据图1可知,
解:根据图1可知,∵△ABC和△ADE是等腰直角三角形,
∴∠CAB=45°,
即△ABC绕点A逆时针旋转45°可到△ADE;
如右图,
∵△ABC和△ADE是等腰直角三角形,
∴∠DAE=∠CAB=45°,
∴∠FAB=∠DAE+∠CAB=90°,
即图1可以逆时针连续旋转90°得到图2.
故选A.
点评:本题考查了旋转的性质、等腰直角三角形的性质,解题的关键是理解旋转的性质,能找对旋转中心、旋转角.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 15、如图,在△ABC和△DEF中,已知AB=DE,AC=DF,要使△ABC≌△DEF,根据三角形全等的判定公理还需添加条件(填上你认为正确的一种情况)
15、如图,在△ABC和△DEF中,已知AB=DE,AC=DF,要使△ABC≌△DEF,根据三角形全等的判定公理还需添加条件(填上你认为正确的一种情况)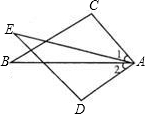 如图:在△ABC和△ADE中,已知∠1=∠2,∠B=∠E,AC=AD.请说明△ABC≌△AED的理由.
如图:在△ABC和△ADE中,已知∠1=∠2,∠B=∠E,AC=AD.请说明△ABC≌△AED的理由.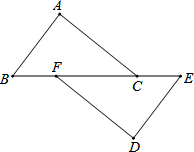 (2013•上海)如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是
(2013•上海)如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 如图,在△ABC和△ADE中,∠DAB=∠EAC,∠C=∠E.
如图,在△ABC和△ADE中,∠DAB=∠EAC,∠C=∠E. 如图,在△ABC和△EFD中,AB=EF,AC=ED,点B,D,C,F在一条直线上.
如图,在△ABC和△EFD中,AB=EF,AC=ED,点B,D,C,F在一条直线上.