Question

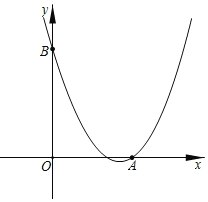
【题目】如图，已知二次函数y＝ax2+bx+c（a≠0）的图象与直线AB相交，与x轴、y轴交于A（2，0）、B（0，2）．

（1）求点O关于AB的对称点P的坐标；

（2）若点P在二次函数y＝ax2+bx+c（a≠0）的图象上，求二次函数y＝ax2+bx+c（a≠0）的关系式．

（3）在（2）的条件下，在△ABP内存在点M，使得MA+MB+MP的值最小，则相应点M的坐标为　 ．

Answer 1

【答案】（1）点P（3，）；（2）y＝﹣x2+x+2；（3）点M坐标为（，），

【解析】

（1）由tan∠BAO==，则∠BAO=60°，GA=OA=1，由∠GAP=∠PAH，得AH=AG=1，则PH=AHtan60°=，即可求解；

（2）将点A、B、P的坐标代入二次函数表达式，即可求解；

（3）△ABP为直角三角形，当点M与点G重合时，MA+MB+MP的值最小，即可求解．

（1）连接AB，过点O作OP⊥AB交AB于点G，过点P作PH⊥x轴于点H，

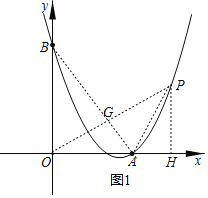
∵点O关于AB的对称点P，∴OG＝PG，

tan∠BAO＝＝，则∠BAO＝60°，

则∠GOA＝∠OAB＝30°，∠GAO＝∠GAP＝∠PAH＝60°，

则GA＝OA＝1，∵∠GAP＝∠PAH，∴AH＝AG＝1，

则PH＝AHtan60°＝，

故点P（3，）；

（2）将点A、B、P的坐标代入二次函数表达式得：

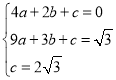，解得：，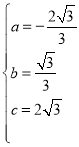

故抛物线的表达式为：y＝﹣x2+x+2；

（3）连接PB，

由题意得：AB＝4，AP＝2，BP＝，

则△ABP为直角三角形，

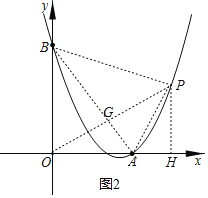
当点M与点G重合时，MA+MB+MP的值最小，

点M坐标为（，），

故答案为：（，）．