题目内容
【题目】如图,点![]() 是∠
是∠![]() 内的一点,过点
内的一点,过点![]() 作
作![]() 于点
于点![]() 于点
于点![]() ,且
,且![]() .
.
![]() 求证:
求证: ![]() ;
;
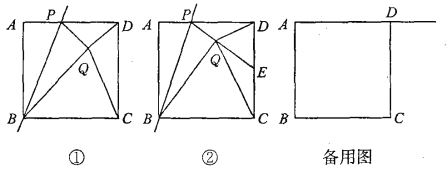
![]() 如图②,点
如图②,点![]() 是射线
是射线![]() 上一点,点
上一点,点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,若
,若![]() .求线段
.求线段![]() 的长.
的长.
![]() 如图③,若
如图③,若![]() ,将
,将![]() 绕点
绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,
的速度顺时针旋转,![]() 秒后,
秒后,![]() 开始绕点
开始绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,
的速度顺时针旋转,![]() 旋转
旋转![]() 后停止,此时
后停止,此时![]() 也随之停止旋转。旋转过程中,
也随之停止旋转。旋转过程中,![]() 所在直线与
所在直线与![]() 所在直线的交点记为
所在直线的交点记为![]() 所在直线与
所在直线与![]() 所在直线的交点记为
所在直线的交点记为![]() .问
.问![]() 旋转几秒时,
旋转几秒时,![]() ?
?

【答案】(1)见解析;(2)6.5;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)首先连接![]() ,根据题意,可得∠PBO=∠PAO=90°,由HL可判定Rt△PAO≌Rt△PBO,即可得出PA=PB;
,根据题意,可得∠PBO=∠PAO=90°,由HL可判定Rt△PAO≌Rt△PBO,即可得出PA=PB;
(2)首先证明∠APB=∠CPD,进而得出∠BPD=∠APC,从而可判定![]() ,得出
,得出![]() ,再设
,再设![]() ,列出关系式,即可得解;
,列出关系式,即可得解;
(3)首先设![]() 旋转时间为
旋转时间为![]() 秒,根据题意,由
秒,根据题意,由![]() 推出
推出![]() ,从而得到
,从而得到![]() ,分四种情况讨论:①当
,分四种情况讨论:①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,④当
时,④当![]() 时,分别根据
时,分别根据![]() 列出关于t的关系式,即可得出不同情况下的t值.
列出关于t的关系式,即可得出不同情况下的t值.
(1)证明:连接![]() ,如图所示
,如图所示

![]()
![]() 在
在![]() 和
和![]() 中
中
![]()
![]()
![]()
(2)∵![]()
∴![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]() 在Rt
在Rt![]() 和Rt
和Rt![]() 中
中
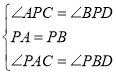
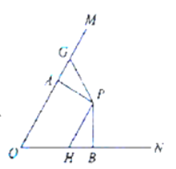
∴![]()
∴![]()
设![]()
则![]() ,
,![]()
![]()
![]()
![]()
![]() 设
设![]() 旋转时间为
旋转时间为![]() 秒,
秒,
①当![]() 时,不存在;
时,不存在;
②当![]() ,如下图
,如下图![]() ,
,![]()
当![]() 时,
时,![]() ,可得
,可得![]()
![]()
![]()
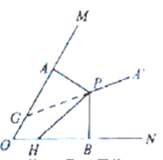
③当![]() 时,如下图
时,如下图
![]()
![]() ,
, ![]()
当![]() 时,
时,![]() ,可得
,可得![]()
![]()
![]() ,
,
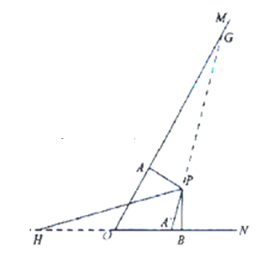
④当![]() 时,如下图
时,如下图
![]() ,
, ![]() ,
,
当![]() 时,
时,![]() ,可得
,可得![]()
∴![]()
![]() ,
,
综上:当![]() 时
时![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目