题目内容
13. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=4,CD=1,则EC的长为$\sqrt{13}$.
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=4,CD=1,则EC的长为$\sqrt{13}$.
分析 首先连接BE,由⊙O的半径OD⊥弦AB于点C,AB=4,CD=1,根据垂径定理可求得AC=BC=2,然后设OA=x,利用勾股定理可得方程:22+(x-1)2=x2,则可求得半径的长,继而利用三角形中位线的性质,求得BE的长,又由AE是直径,可得∠B=90°,继而求得答案.
解答 解:连接BE,
∵⊙O的半径OD⊥弦AB于点C,AB=2,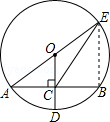
∴AC=BC=2,
设OA=x,
∵CD=1,
∴OC=x-1,
在Rt△AOC中,AC2+OC2=OA2,
∴22+(x-1)2=x2,
解得:x=$\frac{5}{2}$,
∴OA=OE=$\frac{5}{2}$,OC=$\frac{3}{2}$,
∴BE=2OC=3,
∵AE是直径,
∴∠B=90°,
∴CE=$\sqrt{{BC}^{2}{+BE}^{2}}$=$\sqrt{{2}^{2}{+3}^{2}}$=$\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 此题考查了圆周角定理、垂径定理、勾股定理以及三角形中位线的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
4.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数,设个位数字为x,十位数字为y,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=8}\\{xy+18=yx}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=8}\\{10(x+y)+18=yx}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=8}\\{10x+y+18=yx}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=8}\\{x+10y+18=10x+y}\end{array}\right.$ |
2.下列说法正确的是( )
| A. | 抛一枚图钉钉尖着地和钉尖朝上的概率一样大 | |
| B. | 彩票中奖的机会是1%,买100张一定会中奖 | |
| C. | 天气预报说明天下雨的概率是50%,所以明天将有一半的时间在下雨 | |
| D. | 在同一年出生的367名学生中,至少有两人的生日是同一天 |
 某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题:
某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题: 三个等边三角形的摆放位置如图所示,若∠3=60°,则∠1+∠2=120°.
三个等边三角形的摆放位置如图所示,若∠3=60°,则∠1+∠2=120°.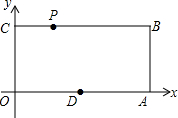 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.