题目内容
【题目】本题满分11分．
如图，已知直线y=-
x +3分别与x、y轴交于点A和B．
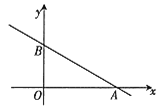
（1）求点A、B的坐标；
（2）求原点O到直线l的距离；
（3）若圆M的半径为2，圆心M在y轴上，当圆M与直线l相切时，求点M的坐标．
【答案】（1）A（4，0）、B（0，3）（2）
（3）M（0，
）或 M（0，
）
【解析】
（1）根据x轴、y轴上的点的特点可以直接求解；
（2）根据点到直线的距离是点到直线的垂线段的长，因此过点O作OC⊥AB于点C，然后根据三角形的面积法可求得距离；
（3）过M作MD⊥AB交AB于点D，然后可通过三角形相似可直接结果，但是由于M点在y轴上移动，因此可知在直线的上方和下方都会相切，因此分两种情况讨论求解．
解：（1）当x=0时，y=3
∴B点坐标（0，3）
当y=0时，有0=-
x + 3，
解得x=4
∴A点坐标为（4，0）
（2）过点O作OC⊥AB于点C，
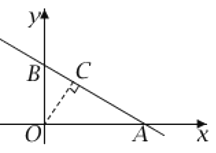
则OC长为原点O到直线l的距离
在Rt△BOA中，0A=4，0B=3，由勾股定理可得AB=5，
∵S△BOA=OB×OA=AB×OC
∴OC=
=
∴原点O到直线l的距离为
（3）
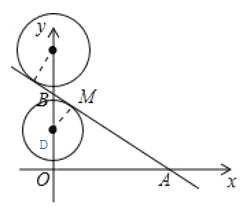
过M作MD⊥AB交AB于点D，当圆M与直线l相切时，MD=2，
在△BOA和△BDM中，
∵∠OBA=∠DBM，∠BOA=∠BDM
∴△BOA∽△BDM
∴
=
，
∴BM=
=
∴ OM=OB–BM=
或OM=OB+ BM=
∴点M的坐标为M（0，）或 M（0，
）
练习册系列答案
相关题目
