��Ŀ����
��ͼ��������y=��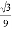 x2+
x2+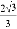 x+3
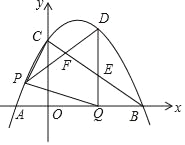
x+3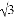 ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C������AC��BC����P��AC��ÿ��1����λ���ȵ��ٶ��ɵ�A���C�˶���ͬʱ����Q��BO��ÿ��2����λ���ȵ��ٶ��ɵ�B���O�˶�����һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶�������PQ������Q��QD��x�ᣬ�������߽��ڵ�D����BC���ڵ�E������PD����BC���ڵ�F�����P���˶�ʱ��Ϊt�루t��0����
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C������AC��BC����P��AC��ÿ��1����λ���ȵ��ٶ��ɵ�A���C�˶���ͬʱ����Q��BO��ÿ��2����λ���ȵ��ٶ��ɵ�B���O�˶�����һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶�������PQ������Q��QD��x�ᣬ�������߽��ڵ�D����BC���ڵ�E������PD����BC���ڵ�F�����P���˶�ʱ��Ϊt�루t��0����
��1����ֱ��BC�ĺ�������ʽ��
��2����ֱ��д��P��D��������꣨�ú�t�Ĵ���ʽ��ʾ������軯��
���ڵ�P��Q�˶��Ĺ����У���PQ=PDʱ����t��ֵ��
��3����̽���ڵ�P��Q�˶��Ĺ����У��Ƿ����ijһʱ�̣�ʹ�õ�FΪPD���е㣿�����ڣ���ֱ��д����ʱt��ֵ���F�����ꣻ�������ڣ���˵�����ɣ�
 �Ķ��쳵ϵ�д�
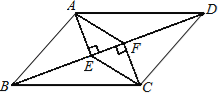
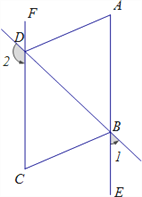
�Ķ��쳵ϵ�д���ͼ����֪��ABC�͡�ADE��Ϊ�ȱ������Σ�D��BC�ϣ�DE��AC�ཻ�ڵ�F��AB=9��BD=3����CF���ڣ�������

A. 1 B. 2 C. 3 D. 4
ij��ѧ���������15��ѧ�����˽�����һ����У�μ���������ʱ�䣬�б����£�
����ʱ�䣨Сʱ�� | 5 | 6 | 7 | 8 |
���� | 2 | 6 | 5 | 2 |
����15��ͬѧһ����У�μ���������ʱ�����λ���������ֱ��ǣ� ��
A��6��7 B��7��7 C��7��6 D��6��6


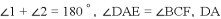 ƽ��
ƽ��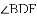
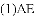
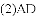
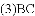
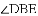
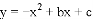 �����㣬�������ߵĶԳ�����_______.
�����㣬�������ߵĶԳ�����_______.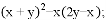

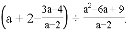
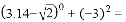 _____��
_____��