题目内容
已知:直线y= x-6与x轴、y轴分别交于A、B两点:
x-6与x轴、y轴分别交于A、B两点:
(1)求A、B两点的坐标;
(2)将该直线沿y轴向上平移6个单位后的图象经过C(-6,a)、D(6,b)两点,分别求a和b的值;
(3)直线y=kx将四边形ABCD的面积分成1:2两部分,求k的值.
解:(1)当x=0时,y=-6,则B点的坐标为:(0,-6);
当y=0时,x=12,则点A的坐标为:(12,0);
(2)由题意得直线CD的解析式为:y= x,
x,
∵点C(-6,a)在函数图象上,
∴a= ×(-6)=-3;
×(-6)=-3;
∵点D(6,b)在函数图象上,
∴b= ×6=3;
×6=3;
综上可得点C的坐标为:(-6,-3),点D的坐标为:(6,3).
(3)
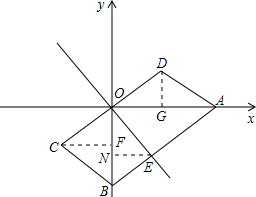
设直线y=kx交线段AB于点E,
则S△ABO= OA×OB=36,S△CBO=
OA×OB=36,S△CBO= CF×OB=18,S△ADO=
CF×OB=18,S△ADO= OA×DG=18,
OA×DG=18,
即可得S四边形ABCD=72,
设△EBO的面积=s,则△AEO的面积=36-s,四边形COBE的面积为18+s,四边形ODAE的面积为54-s,
①若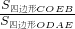 =
= ,则
,则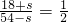 ,
,
解得:s=6,
则 ×OB×xE=6,
×OB×xE=6,
解得;xE=2,
代入直线AB的解析式y= x-6,可得yE=-5,
x-6,可得yE=-5,
∵点E(2,-5)在直线y=kx上,
∴-5=2k,
解得:k=- ;
;
②若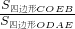 =2,则
=2,则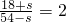 ,
,
解得:s=30,
则 ×OB×xE=30,
×OB×xE=30,
解得;xE=10,
代入直线AB的解析式y= x-6,可得yE=-1,
x-6,可得yE=-1,
∵点E(10,-1)在直线y=kx上,
∴-1=10k,
解得:k=- ;
;
综上可得k的值为- 或-
或- .
.
分析:(1)根据直线解析式可得出A、B的坐标;
(2)先确定平移后的解析式,然后将点C、点D的坐标代入可得出a和b的值;
(3)先画出图形,将四边形ABCD的面积分为三个三角形的面积,然后根据被分为的两部分的面积之比为1:2,可得出点E的坐标,继而可得出k的值.
点评:本题属于一次函数综合题,涉及了一次函数的几何变换、一次函数图象上点的坐标特征,及不规则图形的面积求解,难点在第三问,注意将四边形的面积分割求解,难度较大.
当y=0时,x=12,则点A的坐标为:(12,0);
(2)由题意得直线CD的解析式为:y=
 x,
x,∵点C(-6,a)在函数图象上,
∴a=
 ×(-6)=-3;
×(-6)=-3;∵点D(6,b)在函数图象上,
∴b=
 ×6=3;
×6=3;综上可得点C的坐标为:(-6,-3),点D的坐标为:(6,3).
(3)

设直线y=kx交线段AB于点E,
则S△ABO=
 OA×OB=36,S△CBO=
OA×OB=36,S△CBO= CF×OB=18,S△ADO=
CF×OB=18,S△ADO= OA×DG=18,
OA×DG=18,即可得S四边形ABCD=72,
设△EBO的面积=s,则△AEO的面积=36-s,四边形COBE的面积为18+s,四边形ODAE的面积为54-s,
①若
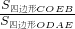 =
= ,则
,则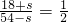 ,
,解得:s=6,
则
 ×OB×xE=6,
×OB×xE=6,解得;xE=2,
代入直线AB的解析式y=
 x-6,可得yE=-5,
x-6,可得yE=-5,∵点E(2,-5)在直线y=kx上,
∴-5=2k,
解得:k=-
 ;
;②若
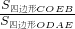 =2,则
=2,则 ,
,解得:s=30,
则
 ×OB×xE=30,
×OB×xE=30,解得;xE=10,
代入直线AB的解析式y=
 x-6,可得yE=-1,
x-6,可得yE=-1,∵点E(10,-1)在直线y=kx上,
∴-1=10k,
解得:k=-
 ;
;综上可得k的值为-
 或-
或- .
.分析:(1)根据直线解析式可得出A、B的坐标;
(2)先确定平移后的解析式,然后将点C、点D的坐标代入可得出a和b的值;
(3)先画出图形,将四边形ABCD的面积分为三个三角形的面积,然后根据被分为的两部分的面积之比为1:2,可得出点E的坐标,继而可得出k的值.
点评:本题属于一次函数综合题,涉及了一次函数的几何变换、一次函数图象上点的坐标特征,及不规则图形的面积求解,难点在第三问,注意将四边形的面积分割求解,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知:直线y=-
x+
(n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2011=( )
| n |
| n+1 |
| ||
| n+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 19、如图,已知两直线a,b相交于O,∠2=30°,则∠1=
19、如图,已知两直线a,b相交于O,∠2=30°,则∠1= 已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.
已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C. 已知:直线y=kx+b的图象过点A(-3,1);B(-1,2),
已知:直线y=kx+b的图象过点A(-3,1);B(-1,2),