题目内容
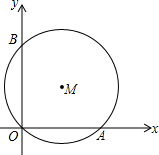 如图,平面直角坐标系中,点A、B分别为x轴和y轴正半轴上的点,设A(a,0),B(0,b),过A、B及原点O作圆,圆心为M.
如图,平面直角坐标系中,点A、B分别为x轴和y轴正半轴上的点,设A(a,0),B(0,b),过A、B及原点O作圆,圆心为M.(1)若a=5,b=12,求圆心M的坐标;
(2)若a、b是关于x的一元二次方程x2-2x+m+1=0的两个实数根,求圆M的半径r的取值范围.
考点:圆的综合题,根的判别式,根与系数的关系,不等式的性质,解一元一次不等式组,垂径定理
专题:综合题
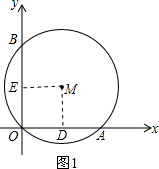
分析:(1)过点M作MD⊥x轴于D,过点M作ME⊥y轴于E,如图1,运用垂径定理就可解决问题.
(2)连接AB,如图2,可得AB是⊙M的直径.由a>0,b>0即可得到a+b>0,ab>0,然后根据根的判别式及根与系数的关系就可求出m的范围,就可解决问题.
(2)连接AB,如图2,可得AB是⊙M的直径.由a>0,b>0即可得到a+b>0,ab>0,然后根据根的判别式及根与系数的关系就可求出m的范围,就可解决问题.
解答:解:(1)过点M作MD⊥x轴于D,过点M作ME⊥y轴于E,如图1.
∵a=5,b=12,
∴OA=5,OB=12.
根据垂径定理可得:OD=AD=
OA=
,OE=BE=
OB=6,
∴圆心M的坐标为(
,6).
(2)连接AB,如图2.
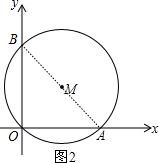
∵∠AOB=90°,
∴AB是⊙M的直径.
∵点A、B分别为x轴和y轴正半轴上的点,∴a>0,b>0.
∵a、b是关于x的一元二次方程x2-2x+m+1=0的两个实数根,
∴
,
解得:-1<m≤0.
在Rt△AOB中,
∵AB2=OA2+OB2,AB=2r,OA=a,OB=b,
∴(2r)2=a2+b2
=(a+b)2-2ab
=4-2(m+1)
=2-2m.
∵-1<m≤0,
∴0≤-2m<2,
∴2≤2-2m<4,
∴2≤4r2<4,
∴
≤r2<1,
∵r>0,
∴
≤r<1.
∴圆M的半径r的取值范围是
≤r<1.

∵a=5,b=12,
∴OA=5,OB=12.
根据垂径定理可得:OD=AD=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
∴圆心M的坐标为(
| 5 |
| 2 |
(2)连接AB,如图2.

∵∠AOB=90°,
∴AB是⊙M的直径.
∵点A、B分别为x轴和y轴正半轴上的点,∴a>0,b>0.
∵a、b是关于x的一元二次方程x2-2x+m+1=0的两个实数根,
∴
|
解得:-1<m≤0.
在Rt△AOB中,
∵AB2=OA2+OB2,AB=2r,OA=a,OB=b,
∴(2r)2=a2+b2
=(a+b)2-2ab
=4-2(m+1)
=2-2m.
∵-1<m≤0,
∴0≤-2m<2,
∴2≤2-2m<4,
∴2≤4r2<4,
∴
| 1 |
| 2 |
∵r>0,
∴
| ||
| 2 |
∴圆M的半径r的取值范围是
| ||
| 2 |
点评:本题主要考查了垂径定理、根的判别式、根与系数的关系、解一元一次不等式组、不等式的性质、完全平方公式、勾股定理等知识,有一定的综合性,而运用根的判别式及根与系数的关系是解决第(2)小题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
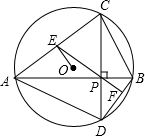 如图,△ABC内接于⊙O,CD⊥AB于P,交⊙O于D,E为AC的中点,EP交BD于F,⊙O的直径为d.下列结论:
如图,△ABC内接于⊙O,CD⊥AB于P,交⊙O于D,E为AC的中点,EP交BD于F,⊙O的直径为d.下列结论:①EF⊥BD;②AC2+BD2的值为定值;③OE=
| 1 |
| 2 |
其中正确的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
娜娜有一个问题请教你,下列图形中对称轴只有两条的是( )
A、 |
B、 |
C、 |
D、 |
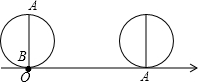 王老师在讲“实数”这节时,做了如下实验:如图所示,AB是半径为1的圆的直径,将B点放在数轴的原点上,将圆沿数轴向右滚动,A点刚好落在数轴上时,A点对应的数为
王老师在讲“实数”这节时,做了如下实验:如图所示,AB是半径为1的圆的直径,将B点放在数轴的原点上,将圆沿数轴向右滚动,A点刚好落在数轴上时,A点对应的数为 如图是一均匀薄板,半径R=30cm,现从板上挖掉一个r=15cm的内切圆,试求剩余薄板的重心C与大圆圆心O的距离.
如图是一均匀薄板,半径R=30cm,现从板上挖掉一个r=15cm的内切圆,试求剩余薄板的重心C与大圆圆心O的距离.
 用小立方块搭成的几何体,主视图和俯视图如下,问这样的几何体有多少可能?它最多要多少小立方块,最少要多少小立方块,画出最多、最少时的左视图.
用小立方块搭成的几何体,主视图和俯视图如下,问这样的几何体有多少可能?它最多要多少小立方块,最少要多少小立方块,画出最多、最少时的左视图.