题目内容
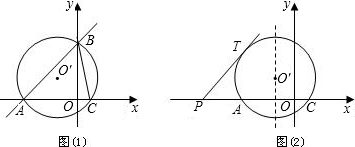
已知PT切⊙O于T，PB为经过圆心的割线交⊙O于点A，（PB＞PA），若PT=4，PA=2，则cos∠BPT=
- A.
- B.
- C.
- D.
A
分析：先画图，设⊙O的半径是x，再利用切割线定理可得PT2=PA•PB，即42=2×（2+2x），易求x，进而可求OP，从而可求
cos∠BPT．
解答：
解：如右图所示，连接OT，设⊙O的半径是x，
∵PT是切线，PB是割线，
∴PT2=PA•PB，
∴42=2×（2+2x），
∴x=3，
∴OP=5，
∴cos∠BPT=
=．
故选A．
点评：本题考查了切割线定理、余弦计算．解题的关键是利用切割线定理求出半径．
分析：先画图，设⊙O的半径是x，再利用切割线定理可得PT2=PA•PB，即42=2×（2+2x），易求x，进而可求OP，从而可求
cos∠BPT．
解答：
解：如右图所示，连接OT，设⊙O的半径是x，∵PT是切线，PB是割线，
∴PT2=PA•PB，
∴42=2×（2+2x），
∴x=3，
∴OP=5，
∴cos∠BPT=
=．故选A．
点评：本题考查了切割线定理、余弦计算．解题的关键是利用切割线定理求出半径．
练习册系列答案
相关题目
点作⊙O的割线PAB（PB＞PA）．设PA=x，PB=y．
15、如图，PT切⊙O于点T，经过圆心O的割线PAB交⊙O于点A、B，已知PT=4，PA=2，则⊙O的直径AB等于（ ）
