题目内容
 在直角三角形ABC中,∠C=90°,BC=2,以AB为边作正方形ABDE,连接AD、BE交O,CO=
在直角三角形ABC中,∠C=90°,BC=2,以AB为边作正方形ABDE,连接AD、BE交O,CO= ,则AC的长为
,则AC的长为
- A.2
- B.3
- C.4
- D.

C
分析:延长CB过点D作CB延长线的垂线,交点为F,过点O作OM⊥CF,先证明RT△ACB≌RT△BFD,然后分别表示出OM、CM的长度,在RT△OCM中利用勾股定理可得出答案.
解答: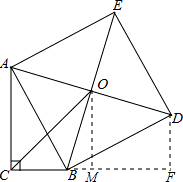
解:延长CB过点D作CB延长线的垂线,交点为F,过点O作OM⊥CF,
则可得OM是梯形ACFD的中位线,
∵∠ABC+∠FBD=∠CAB+∠ABC=90°,
∴∠CAB=∠FBD,
在RT△ACB和RT△BFD中,
∵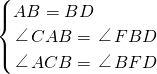 ,
,
∴RT△ACB≌RT△BFD,
∴AC=BF,BC=DF,
设AC=x,则OM=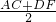 =
=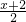 ,CM=
,CM= =
=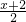 ,
,
在RT△OCM中,OM2+CM2=OC2,即2(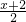 )2=18,
)2=18,
解得:x=4,即AC的长度为4.
故选C.
点评:此题考查了正方形的性质、勾股定理、梯形的中位线定理、全等三角形的判定和性质,解答本题的关键是正确作出辅助线,构造全等三角形,难度较大.
分析:延长CB过点D作CB延长线的垂线,交点为F,过点O作OM⊥CF,先证明RT△ACB≌RT△BFD,然后分别表示出OM、CM的长度,在RT△OCM中利用勾股定理可得出答案.
解答:

解:延长CB过点D作CB延长线的垂线,交点为F,过点O作OM⊥CF,
则可得OM是梯形ACFD的中位线,
∵∠ABC+∠FBD=∠CAB+∠ABC=90°,
∴∠CAB=∠FBD,
在RT△ACB和RT△BFD中,
∵
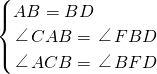 ,
,∴RT△ACB≌RT△BFD,
∴AC=BF,BC=DF,
设AC=x,则OM=
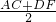 =
=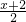 ,CM=
,CM= =
=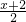 ,
,在RT△OCM中,OM2+CM2=OC2,即2(
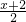 )2=18,
)2=18,解得:x=4,即AC的长度为4.
故选C.
点评:此题考查了正方形的性质、勾股定理、梯形的中位线定理、全等三角形的判定和性质,解答本题的关键是正确作出辅助线,构造全等三角形,难度较大.

练习册系列答案
相关题目
 6、如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC的中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是
6、如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC的中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是 使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M.
使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M. 如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?