Question

（2012•淮安）国家和地方政府为了提高农民种粮的积极性，每亩地每年发放种粮补贴120元．种粮大户老王今年种了150亩地，计划明年再承租50～150亩土地种粮以增加收入，考虑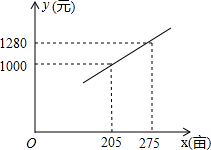各种因素，预计明年每亩种粮成本y（元）与种粮面积x（亩）之间的函数关系如图所示：（1）今年老王种粮可获得补贴多少元？
（2）根据图象，求y与x之间的函数关系式；
（3）若明年每亩的售粮收入能达到2140元，求老王明年种粮总收入W（元）与种粮面积x（亩）之间的函数关系式．当种粮面积为多少亩时，总收入最高？并求出最高总收入．

Answer 1

分析：（1）根据每亩地每年发放种粮补贴120元，种粮大户老王今年种了150亩地，得出老王种粮可获得补贴数目；
（2）利用待定系数法求出一次函数解析式即可；
（3）根据明年每亩的售粮收入能达到2140元，预计明年每亩种粮成本y（元）与种粮面积x（亩）之间的函数关系为y=4x+180，进而得出W与x的函数关系式，再利用二次函数的最值公式求出即可．

解答：解：（1）∵国家和地方政府为了提高农民种粮的积极性，每亩地每年发放种粮补贴120元，种粮大户老王今年种了150亩地，
∴今年老王种粮可获得补贴120×150=18000元；

（2）假设函数解析式为y=kx+b，根据图象可以得出：图象过（205，1000），（275，1280），
将两点代入解析式得出：

205k+b=1000 275k+b=1280

，
解得：

k=4 b=180

，
则y与x之间的函数关系式为：y=4x+180；

（3）根据题意得出：
W=（2140-y）x+120x
=[2140-（4x+180）]x+120x
=-4x²+1960x+120x
=-4x²+2080x，
则x=-

b

2a

=-

2080

2×(-4)

=260时，
∵x≥150+50，x≤150+150，
∴200≤x≤300，
W最大=

4ac-b2

4a

=270400（元）．
当种粮面积为260亩时，总收入最高为270400元．

点评：此题主要考查了一次函数的应用以及待定系数法求一次函数解析式和二次函数的最值问题，根据已知得出W与x的函数关系式是解题关键．