题目内容
(1)先因式分解在求值.(m2+n2)-4m2n2,其中m=-3,n=2.
(2)先化简,再求值.(1-
)÷
,其中a是整数,且-3<a<3.
(2)先化简,再求值.(1-
| 1 |
| a-1 |
| a2-4 |
| a2-a |
考点:分式的化简求值,因式分解-运用公式法
专题:
分析:(1)首先利用乘法公式分解因式,进而将已知代入求出即可;
(2)首先通分进而利用分式乘法运算法则化简求出即可.
(2)首先通分进而利用分式乘法运算法则化简求出即可.
解答:解:(1)(m2+n2)-4m2n2=(m-n)2-2m2n2=(m-n+
mn)(m-n-
mn)
将m=-3,n=2代入得出:
原式=(-3+2-6
)(-3-2+6
)
=(-1-6
)(-5+6
)
=5-6
+30
-72
=-67+24
;
(2)(1-
)÷
,
=(
-
)×
=
×
=
∵a是整数,且-3<a<3,
∴a=1时,
原式=
=
.
| 2 |
| 2 |
将m=-3,n=2代入得出:
原式=(-3+2-6
| 2 |
| 2 |
=(-1-6
| 2 |
| 2 |
=5-6
| 2 |
| 2 |
=-67+24
| 2 |
(2)(1-
| 1 |
| a-1 |
| a2-4 |
| a2-a |
=(
| a-1 |
| a-1 |
| 1 |
| a-1 |
| a(a-1) |
| (a-2)(a+2) |
=
| a-2 |
| a-1 |
| a(a-1) |
| (a-2)(a+2) |
=
| a |
| a+2 |
∵a是整数,且-3<a<3,
∴a=1时,
原式=
| 1 |
| 1+2 |
| 1 |
| 3 |
点评:此题主要考查了分式的混合运算以及因式分解,正确分解因式是解题关键.

练习册系列答案
相关题目
关于x的不等式组
的解集在同一数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
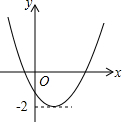 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0有实数根,下列结论:①abc>0;②b2-4ac>0;③m>-2,其中,正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0有实数根,下列结论:①abc>0;②b2-4ac>0;③m>-2,其中,正确的个数是( )| A、0 | B、1 | C、2 | D、3 |
 如图,A、B两点在双曲线y=
如图,A、B两点在双曲线y=| 4 |
| x |
| A、4 | B、2 | C、1 | D、无法确定 |