题目内容
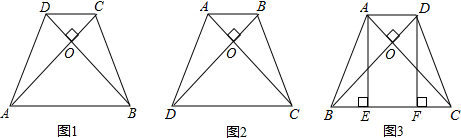
①如图1,在梯形ABCD中,AB∥CD,AD=BC,对角线AC⊥BD,垂足为O.若CD=3,AB=5,则AC的长为
②如图2,在等腰梯形ABCD中,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积为
③如图3,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E、F,AD=4,BC=8,则AE+EF等于
4
| 2 |
4
.| 2 |
②如图2,在等腰梯形ABCD中,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积为
18
18
cm2.③如图3,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E、F,AD=4,BC=8,则AE+EF等于
10
10
.
分析:①求出∠DAB=∠CBA,证△DAB≌△CBA,推出∠DBA=∠CAB=45°,求出OA、OB的值,同理求出OC的值即可;
②证△DAB≌△CBA,求出AC=BD,根据三角形面积公式求出即可;
③过D作DM∥AC交BC的延长线于M,得出平行四边形AEFD和平行四边形ACMD,求出AD=CM=4,求出DF,即可求出AE.
②证△DAB≌△CBA,求出AC=BD,根据三角形面积公式求出即可;
③过D作DM∥AC交BC的延长线于M,得出平行四边形AEFD和平行四边形ACMD,求出AD=CM=4,求出DF,即可求出AE.
解答:①解:∵四边形ABCD是等腰梯形,
∴∠DAB=∠CBA,
在△DAB和△CBA中,
∵
,
∴△DAB≌△CBA(SAS),
∴∠DBA=∠CAB,
∵AC⊥BD,
∴∠AOB=90°,
∴∠OAB=∠OBA=45°,
∴OA=OB,
同理OD=OC,
设OA=OB=a,在△AOB中,AB=5,由勾股定理得:a2+a2=52,
a=
,
OA=OB=
,
同理OC=OD=
,
∴AC=OA+OC=
+
=4
,
故答案为:4
.
②解:∵四边形ABCD是等腰梯形,
∴∠DAB=∠CBA,
在△DAB和△CBA中,
∵
,
∴△DAB≌△CBA(SAS),
∴AC=BD=6cm,
∴梯形ABCD的面积是S△ABD+S△CBD
=
×BD×OA+
×BD×OC
=
×BD×(OA+OC)
=
×BD×AC
=18(cm2),
故答案为:18.
③解:过D作DM∥AC交BC的延长线于M,
∵AD∥BC,DM∥AC,
∴四边形ACMD是平行四边形,
∴AD=CM=4,AC=DM,
∵AE⊥BC,DF⊥BC,
∴AE∥DF,
∵AD∥BC,
∴四边形ADFE是平行四边形,
∴AD=EF=4,
∵四边形ABCD是等腰梯形,
∴∠ADC=∠BCD,
在△ABC和△DCB中,
∵
,
∴△ABC≌△DCB(SAS),
∴AC=BD,
∴BD=DM,
∵DM∥AC,AC⊥BD,
∴∠MDB=90°,
∵DF⊥BM,BD=DM,
∴BF=FM,
∴DF=
BM=
×(4+8)=6,
∵AE⊥BC,DF⊥BC,
∴AF∥DF,
∵AD∥BC,
∴四边形AEFD是平行四边形,
∴AE=DF=6,
∴AE+EF=6+4=10,
故答案为:10.
∴∠DAB=∠CBA,
在△DAB和△CBA中,
∵
|
∴△DAB≌△CBA(SAS),
∴∠DBA=∠CAB,
∵AC⊥BD,
∴∠AOB=90°,
∴∠OAB=∠OBA=45°,
∴OA=OB,
同理OD=OC,
设OA=OB=a,在△AOB中,AB=5,由勾股定理得:a2+a2=52,
a=
5
| ||
| 2 |
OA=OB=
5
| ||
| 2 |
同理OC=OD=
3
| ||
| 2 |
∴AC=OA+OC=
3
| ||
| 2 |
5
| ||
| 2 |
| 2 |
故答案为:4
| 2 |
②解:∵四边形ABCD是等腰梯形,
∴∠DAB=∠CBA,
在△DAB和△CBA中,
∵
|
∴△DAB≌△CBA(SAS),
∴AC=BD=6cm,
∴梯形ABCD的面积是S△ABD+S△CBD
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=18(cm2),
故答案为:18.

③解:过D作DM∥AC交BC的延长线于M,
∵AD∥BC,DM∥AC,
∴四边形ACMD是平行四边形,
∴AD=CM=4,AC=DM,
∵AE⊥BC,DF⊥BC,
∴AE∥DF,
∵AD∥BC,
∴四边形ADFE是平行四边形,
∴AD=EF=4,
∵四边形ABCD是等腰梯形,
∴∠ADC=∠BCD,
在△ABC和△DCB中,
∵
|
∴△ABC≌△DCB(SAS),
∴AC=BD,
∴BD=DM,
∵DM∥AC,AC⊥BD,
∴∠MDB=90°,
∵DF⊥BM,BD=DM,
∴BF=FM,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
∵AE⊥BC,DF⊥BC,
∴AF∥DF,
∵AD∥BC,
∴四边形AEFD是平行四边形,
∴AE=DF=6,
∴AE+EF=6+4=10,
故答案为:10.
点评:本题考查了等腰梯形的性质,平行四边形的性质和判定,直角三角形斜边上中线性质,勾股定理等知识点的综合运用,题目都比较好,综合性比较强.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目


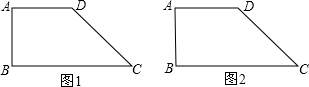 如图1,在梯形ABCD中,AD∥BC,AD=2,BC=4.AB=2,CD=2
如图1,在梯形ABCD中,AD∥BC,AD=2,BC=4.AB=2,CD=2