题目内容
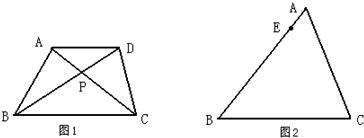
如图1,在梯形ABCD中,AD∥BC,且BC=12cm,AD=15cm,动点Q由点B沿BC向点C移动,1秒钟后动点P由点A沿AD向点D移动(1)若动点P的速度比动点Q的速度大1厘米/秒,且动点Q到达C时,动点P 恰好也到达D.试求动点P、Q的速度.
(2)若动点P的速度为5厘米/秒,动点Q的速度为3厘米/秒,在运动过程中(P与A、D不重合时),AQ与BP交于K,CP与DQ交于N
①当动点Q到达BC中点时,过K作KM∥AD交AB于M,求KM的长;(如图2)
②在这运动过程中,KN是否会与AD平行?若会,请求出此时为P点出发后几秒?若不会,请说明理由.(如图3)

分析:(1)首先设动点Q的速度为x厘米/秒,根据题意即可得方程:
=
+1,解此方程即可求得答案,注意分式方程需检验;
(2)①由动点Q到达BC中点,即可求得BQ与AP的值,又由MK∥AD∥BC,根据平行线分线段成比例定理,即可求得MK的值;
②首先设点P点出发后t秒时,KN∥AD,然后根据平行线分线段成比例定理与比例的性质,即可得方程
=
’又由此方程无解,即可证得KN不会平行于AD.
| 12 |
| x |
| 15 |
| x+1 |
(2)①由动点Q到达BC中点,即可求得BQ与AP的值,又由MK∥AD∥BC,根据平行线分线段成比例定理,即可求得MK的值;
②首先设点P点出发后t秒时,KN∥AD,然后根据平行线分线段成比例定理与比例的性质,即可得方程
| 3(t+1) |
| 5t |
| 12-3(t+1) |
| 15-5t |
解答:解:(1)设动点Q的速度为x厘米/秒,
根据题意得:
=
+1,
解得:x1=2,x2=-6(不合题意舍去)
经检验x=2是原方程根,
∴动点Q速度为2厘米/秒,动点P速度为3厘米/秒.
(2)①当BQ=
BC=6cm时,AP=5×(6÷3-1)=5cm,
由MK∥AD∥BC,
得
=
=
,
=
=
,
∴MK=
cm;
②设点P点出发后t秒时,KN∥AD,
∴
=
=
,
=
=
,
若KN∥AD,则
=
’
解得:
=1此方程无解,
∴KN不会平行于AD.
根据题意得:
| 12 |
| x |
| 15 |
| x+1 |
解得:x1=2,x2=-6(不合题意舍去)
经检验x=2是原方程根,
∴动点Q速度为2厘米/秒,动点P速度为3厘米/秒.
(2)①当BQ=
| 1 |
| 2 |
由MK∥AD∥BC,
得
| BK |
| KP |
| BQ |
| AP |
| 6 |
| 5 |
| MK |
| AP |
| BK |
| BP |
| 6 |
| 11 |
∴MK=
| 30 |
| 11 |
②设点P点出发后t秒时,KN∥AD,
∴
| QK |
| KA |
| BQ |
| AP |
| 3(t+1) |
| 5t |
| QN |
| ND |
| CQ |
| DP |
| 12-3(t+1) |
| 15-5t |
若KN∥AD,则
| 3(t+1) |
| 5t |
| 12-3(t+1) |
| 15-5t |
解得:
| t+1 |
| t |
∴KN不会平行于AD.
点评:此题考查了平行线分线段成比例定理,分式方程的解法,以及比例的性质等知识.此题综合性较强,难度较大,解题的关键是注意比例的性质与比例变形,注意数形结合思想的应用.

练习册系列答案
相关题目

 24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是
24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是

