Question

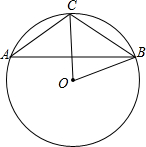如图，已知A、B、C是⊙O上的三个点，且AB=15cm，AC=3

3

cm，∠BOC=60度．如果D是线段BC上的点，且点D到直线AC的距离为2cm，那么BD=

 

cm．

Answer 1

分析：作BF⊥AC于F，构造出特殊的直角三角形，计算有关线段的长度；根据DE∥BF得比例线段求解．

解答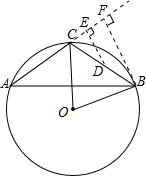：解：作DE⊥AC于E，BF⊥AC于F
∵∠BOC=60°，∴∠A=30°
在Rt△ABF中，AB=15cm
∴BF=

15

2

cm，AF=

15 3

2

cm
∴CF=AF-AC=

15 3

2

-3

3

=

9 3

2

cm
在Rt△BCF中，BC=

( 15 2 )2+( 9 3 2 )2

=3

13

cm
∵DE∥BF
∴

DE

BF

=

CD

BC

设BD=x，则

2

15 2

=

3 13 -x

3 13

解得x=

11 13

5

，即BD=

11 13

5

cm．

点评：本题主要考查了圆周角定理，同弧所对的圆周角是同弧所对的圆心角的一半．构造特殊三角形是关键．