题目内容
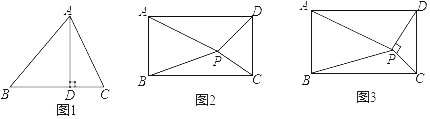
【题目】已知:△ABC中,点D为边BC上一点,点E在边AC上,且∠ADE=∠B
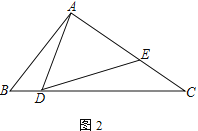
(1) 如图1,若AB=AC,求证:![]() ;
;
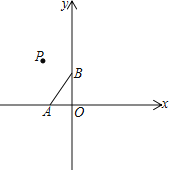
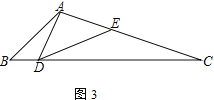
(2) 如图2,若AD=AE,求证:![]() ;
;
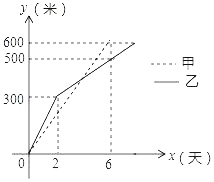
(3) 在(2)的条件下,若∠DAC=90°,且CE=4,tan∠BAD=![]() ,则AB=____________.
,则AB=____________.
【答案】![]()
【解析】分析:(1)![]()
![]()
∠ADE=∠B,可得![]()
![]() 根据等边对等角得到
根据等边对等角得到![]()
△BAD∽△CDE,根据相似三角形的性质即可证明.
(2) 在线段AB上截取DB=DF,证明△AFD∽△DEC,根据相似三角形的性质即可证明.
(3) 过点E作EF⊥BC于F,根据tan∠BAD=tan∠EDF=![]() ,设EF=x,DF=2x,则DE=
,设EF=x,DF=2x,则DE=![]() ,证明△EDC∽△GEC,求得
,证明△EDC∽△GEC,求得![]() ,根据CE2=CD·CG,求出CD=
,根据CE2=CD·CG,求出CD=![]() ,
,
根据△BAD∽△GDE,即可求出![]() 的长度.
的长度.
详解:(1) ![]()
![]()
∠ADE=∠B,可得![]()
![]()
![]()
![]()
∵△BAD∽△CDE,
∴![]() ;
;
(2) 在线段AB上截取DB=DF
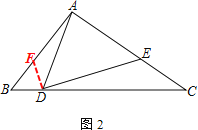
∴∠B=∠DFB=∠ADE
∵AD=AE ∴∠ADE=∠AED ∴∠AED=∠DFB,
同理:∵∠BAD+∠BDA=180°-∠B,∠BDA+∠CDE=180°-∠ADE
∴∠BAD=∠CDE
∵∠AFD=180°-∠DFB,∠DEC=180°-∠AED
∴∠AFD=∠DEC ,
∴△AFD∽△DEC,
∴![]()
(3) 过点E作EF⊥BC于F
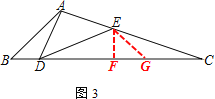
∵∠ADE=∠B=45°
∴∠BDA+∠BAD=135°,∠BDA+∠EDC=135°
∴∠BAD=∠EBC(三等角模型中,这个始终存在)
∵tan∠BAD=tan∠EDF=![]()
∴设EF=x,DF=2x,则DE=![]() ,
,
在DC上取一点G,使∠EGD=45°,
∴△BAD∽△GDE,
∵AD=AE∴∠AED=∠ADE=45°,
∵∠AED=∠EDC+∠C=45°,∠C+∠CEG=45°,∴∠EDC=∠GEC,
∴△EDC∽△GEC,∴![]() ∴
∴![]() ,
,![]()
又CE2=CD·CG,
∴42=CD·![]() ,CD=
,CD=![]() ,
,
∴![]() ,解得
,解得![]()
∵△BAD∽△GDE
∴![]() ,
,
∴![]() .
.

 寒假学与练系列答案
寒假学与练系列答案