题目内容
过线段AB的两端作AC⊥AB于A，BD⊥AB于B，连AD、BC交于O，AC=a，BD=b（b＞a），那么点O到线段AB的距离为分析：分①AC，BD在AB的两侧；②AC、BD在AB的同侧两种情况，根据平行线分线段成比例定理以及比例的性质进行变形即可得到答案．
解答：
解：①如图，若AC，BD在AB的两侧，作OP⊥AB交BA延长线于P，则OP∥CA∥BD，
所以OP：DB=AO：AD
而AO：DO=CA：DB=a：b
所以AO：AD=a：（b-a）
所以OP：b=a：（b-a）
所以OP=
；
②如图，若AC、BD在AB的同侧
作OP⊥AB于P，则CA∥OP∥BD
因为OP：DB=AO：AD
AO：DO=CA：DB=a：b
所以AO：AD=a：（a+b）
所以OP：b=a：（a+b）
所以OP=
．
故答案为：
或
．
解：①如图，若AC，BD在AB的两侧，作OP⊥AB交BA延长线于P，则OP∥CA∥BD，所以OP：DB=AO：AD
而AO：DO=CA：DB=a：b
所以AO：AD=a：（b-a）
所以OP：b=a：（b-a）
所以OP=
| ab |
| b-a |
②如图，若AC、BD在AB的同侧作OP⊥AB于P，则CA∥OP∥BD
因为OP：DB=AO：AD
AO：DO=CA：DB=a：b
所以AO：AD=a：（a+b）
所以OP：b=a：（a+b）
所以OP=
| ab |
| a+b |
故答案为：
| ab |
| a+b |
| ab |
| b-a |
点评：此题主要考查平行线分线段成比例定理的理解及运用．注意本题有两种情况，不要漏掉其中一种．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
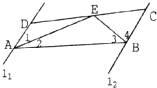22、如图所示，过线段AB的两端作直线l1∥l2，作同旁内角的平分线交于点E，过点E作直线DC分别和直线l1、l2交点D、C，且点D、C在AB的同侧，与A、B不重合．
，作同旁内角的平分线交于点E，过点E作直线DC分别和直线
、
交点D、C，且点D、C在AB的同侧，与A、B不重合．