题目内容
如图，正方形ABCD中，点EF分别在BC、CD上，△AEF是等边三角形，连AC交EF于G，下列结论：①∠BAE=∠DAF=15°；②AG=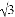
GC；③BE+DF=EF；④S△CEF=2S△ABE，其中正确的个数为（ ）
A. 1 B. 2 C. 3 D. 4
练习册系列答案
相关题目
题目内容
如图，正方形ABCD中，点EF分别在BC、CD上，△AEF是等边三角形，连AC交EF于G，下列结论：①∠BAE=∠DAF=15°；②AG=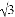GC；③BE+DF=EF；④S△CEF=2S△ABE，其中正确的个数为（ ）
A. 1 B. 2 C. 3 D. 4
x﹣6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．
|﹣（
）﹣1+（2008﹣π）0﹣
tan45°．
